Deep Learning: Basic Mathematics for Deep Learning
স্নায়বিক নেটওয়ার্ক এবং গভীর শেখার সাথে শুরু করার আগে সেগুলি বোঝার জন্য প্রয়োজনীয় মৌলিক গণিত সম্পর্কে আলোচনা করা যাক। আমি গণিতের কিছু গুরুত্বপূর্ণ বিষয় কভার করার চেষ্টা করব যা গভীর শিক্ষার আরও বিষয়গুলি বোঝার প্রয়োজন হবে। এই নিবন্ধে Deep Learning Book সংক্ষিপ্ত নোট রয়েছে।
LINEAR ALGEBRA
লিনিয়ার বীজগণিত পৃথক গণিতের চেয়ে ক্রমাগত একটি ফর্ম, অনেক কম্পিউটার বিজ্ঞানী এটির সাথে খুব কম অভিজ্ঞতা অর্জন করেন little লিনিয়ার বীজগণিত সম্পর্কে একটি ভাল বোঝা অনেকগুলি মেশিন লার্নিং অ্যালগরিদমগুলি বিশেষত গভীর শেখার অ্যালগরিদমগুলি বোঝার জন্য এবং কাজ করার জন্য প্রয়োজনীয়।
লিনিয়ার বীজগণিতের অধ্যয়নের মধ্যে বিভিন্ন ধরণের গাণিতিক বিষয়গুলি অন্তর্ভুক্ত রয়েছে যা তারা নিম্নরূপ:
- Scalars: রৈখিক বীজগণিত/linear algebra অধ্যয়ন করা অন্যান্য বেশিরভাগ অবজেক্টের বিপরীতে একটি স্কেলার কেবল একটি একক সংখ্যা, যা সাধারণত একাধিক সংখ্যার arrays হয়। আমরা italics গুলিতে স্কেলার লিখি। আমরা সাধারণত scalars lower-case variable এর নাম দিই।
- Vectors: একটি ভেক্টর একটি সংখ্যার অ্যারে। সংখ্যাগুলি সাজানো হয়। আমরা প্রতিটি ক্রমিক সংখ্যার ক্রম অনুসারে তার সূচক দ্বারা সনাক্ত করতে পারি। সাধারণত আমরা ভেক্টরগুলিকে ছোট আকারের অক্ষরে টাইপফেসে লিখিত ছোট ছোট নামগুলি দিয়ে থাকি, যেমন x।
- Matrices: একটি ম্যাট্রিক্স হ'ল 2-D array এর সংখ্যার, সুতরাং প্রতিটি উপাদান কেবল একটির পরিবর্তে দুটি সূচক দ্বারা চিহ্নিত হয়। আমরা সাধারণত ম্যাট্রিক গুলিকে বোল্ড টাইপ ফেসের সাথে upper-case variable এর নাম দিয়ে থাকি, যেমন A
- Tensors:: কিছু ক্ষেত্রে আমাদের আরও দুটি অক্ষ সহ একটি অ্যারের প্রয়োজন।সাধারণ ক্ষেত্রে, নিয়মিত গ্রিডে পরিবর্তনশীল সংখ্যক অক্ষ সহ একটি বিন্যাসের বিন্যাসকে একটি টেনসর হিসাবে পরিচিত।আমরা এই টাইপফেসের সাহায্যে "A" নামক একটি টেনসরকে চিহ্নিত করি A.
ম্যাট্রিক্সে একটি গুরুত্বপূর্ণ অপারেশন হ'ল ট্রান্সপোজ।ম্যাট্রিক্সের স্থানান্তর হ'ল ম্যাট্রিক্সের মিরর চিত্রটি একটি তির্যক রেখা জুড়ে, যাকে প্রধান তির্যক বলা হয়,উপরের বাম কোণ থেকে শুরু করে নীচে এবং ডানদিকে চলমান . আমরা ম্যাট্রিক্স A এর ট্রান্সপোজকে A´ হিসাবে চিহ্নিত করি,এবং এটি ডি-নেড যেমন A´ (i, j) = A (j, i)।
গভীর শিক্ষার প্রসঙ্গে আমরা কিছু কম প্রচলিত স্বরলিপিও ব্যবহার করি আমরা ম্যাট্রিক্স এবং একটি ভেক্টর যুক্ত করার অনুমতি দিই, যা অন্য ম্যাট্রিক্সের ফলন দেয়: C = A + b, যেখানে C (i, j) = A (i, j) + b (j)। অন্য কথায়, ভেক্টর b ম্যাট্রিক্সের প্রতিটি সারিতে যুক্ত করা হয়েছে। এই শর্টহ্যান্ড হ'ল সংযোজন করার আগে প্রতিটি সারিতে কপি করা ম্যাট্রিক্সের b ম্যানের ম্যাট্রিক্সের প্রয়োজনীয়তা দূর করে। অনেক স্থানে b এর এই অনুলিপি সম্প্রচার বলা হয়।
matrix product টির স্থানান্তরের একটি সহজ রূপ রয়েছে: (AB) ´ = B´A´. A-এর ম্যাট্রিক্স বিপরীতকে A ^ -1 হিসাবে চিহ্নিত করা হয়েছে এবং এটি ম্যাট্রিক্স হিসাবে denoted হয়েছে যেমন A ^ -1A = I (I আইডেন্টিটি ম্যাট্রিক্স)। তবে, A^−1 মূলত একটি theoretical tool হিসাবে কার্যকর এবং বেশিরভাগ সফ্টওয়্যার অ্যাপ্লিকেশনগুলির জন্য বাস্তবে ব্যবহার করা উচিত নয় A. কারণ A ^ −1 ডিজিটাল কম্পিউটারে কেবল সীমিত নির্ভুলতার সাথে প্রতিনিধিত্ব করা যেতে পারে, যা অ্যালগরিদমগুলি ব্যবহার করে b এর মান সাধারণত x এর আরও সঠিক অনুমান পেতে পারে।
Some topics that need to be understand.
NORM
আদর্শকখনও কখনও আমাদের একটি size ভেক্টরের পরিমাপ করা প্রয়োজন। মেশিন লার্নিংয়ে আমরা সাধারণত একটি আদর্শ নামক একটি ফাংশন ব্যবহার করে ভেক্টরের size পরিমাপ করি। Given by:
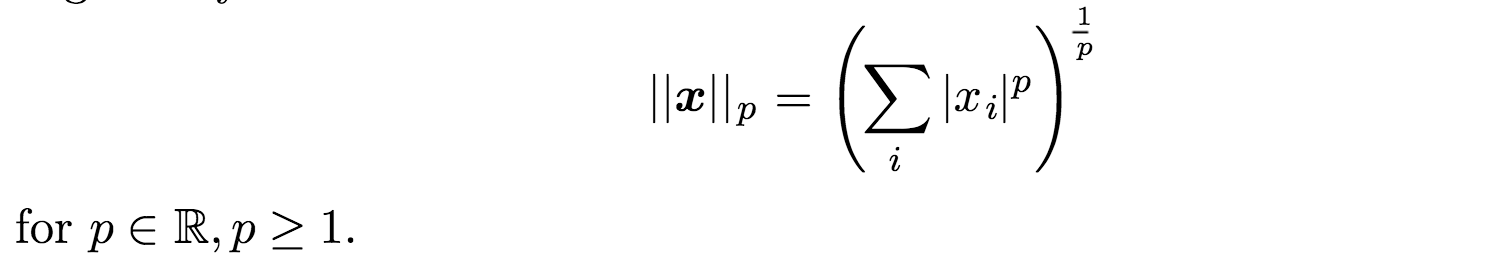
L ^ p আদর্শ সহ অন্যান্য নিয়মগুলি হ'ল ভেক্টরকে non-negative values গুলিতে ম্যাপিং করে। স্বজ্ঞাত স্তরে, একটি ভেক্টর x এর আদর্শটি মূল থেকে বিন্দু x এর দূরত্ব পরিমাপ করে। আরও কঠোরভাবে, একটি আদর্শ হ'ল কোনও বৈশিষ্ট্য যা নীচের বৈশিষ্ট্যগুলি পূরণ করে:
- f (x) = 0 ⇒ x = 0
- f (x + y) ≤ f(x) + f(y) (the triangle inequality)
- ∀α ∈ R, f(αx) = |α|f(x)
সুতরাং আমরা বলতে পারি যে পি L² , p = 2 সহ ইউক্লিডিয়ান আদর্শ হিসাবে পরিচিত কারণ এটি origin/উত্স থেকে কেবল ইউক্লিডিয়ান দূরত্ব।
EIGEN DECOMPOSITION নিজস্ব রক্ষণাবেক্ষণ
অনেক mathematical objects গুলি আরও ভালভাবে বোঝা যায় তাদের উপাদানগুলি ভাঙ্গার মাধ্যমে,তাদের কিছু properties যা সর্বজনীন,আমরা তাদের প্রতিনিধিত্ব করার উপায়টি বেছে না নিয়ে তৈরি করি . উদাহরণস্বরূপ, integers/পূর্ণসংখ্যাগুলি প্রধান কারণগুলিতে decomposed/দ্রবীভূত হতে পারে। আমরা যেভাবে 12 নম্বর প্রতিনিধিত্ব করি তা পরিবর্তিত হবে তার উপর নির্ভর করে আমরা এটি base ten or in binary লিখছি কিনা, তবে এটি সর্বদা সত্য হবে যে 12 = 2 × 2 × 3। এই উপস্থাপনা থেকে আমরা দরকারী বৈশিষ্ট্যগুলি উপস্থাপন করতে পারি, যেমন 12 টি 5 দ্বারা বিভাজ্য নয় বা কোনও পূর্ণসংখ্যা একাধিক বা 12 দ্বারা 3 দ্বারা বিভাজ্য হবে।
একইভাবে আমরা ম্যাট্রিকগুলিকে এমনভাবে decompose করতে পারি যা তাদের functional properties সম্পর্কে তথ্য প্রদর্শন করে। সর্বাধিক ব্যবহৃত শিশু বা ম্যাট্রিক্সের decomposition কে eigen-decomposition বলা হয়, যেখানে আমরা ম্যাট্রিক্সকে একটি সেট বা eigenvectors and eigenvalues তে বিভক্ত করি।
একটি eigenvector ভেেক্টর বা একটি square matrix A হ'ল A-এর দ্বারা গুণিতকরণের একটি non-zero vector কেবল v এর স্কেলকে পরিবর্তিত করে: Av = λv
স্কেলার λএই eigenvector /ইগেনভেক্টরের সাথে সম্পর্কিত eigenvalue/ইগেনভ্যালু হিসাবে পরিচিত।
ইগেনভ্যালু এবং ইগেনভেেক্টরের একটি visual representation চিত্র 1 এ দেখানো হয়েছে।
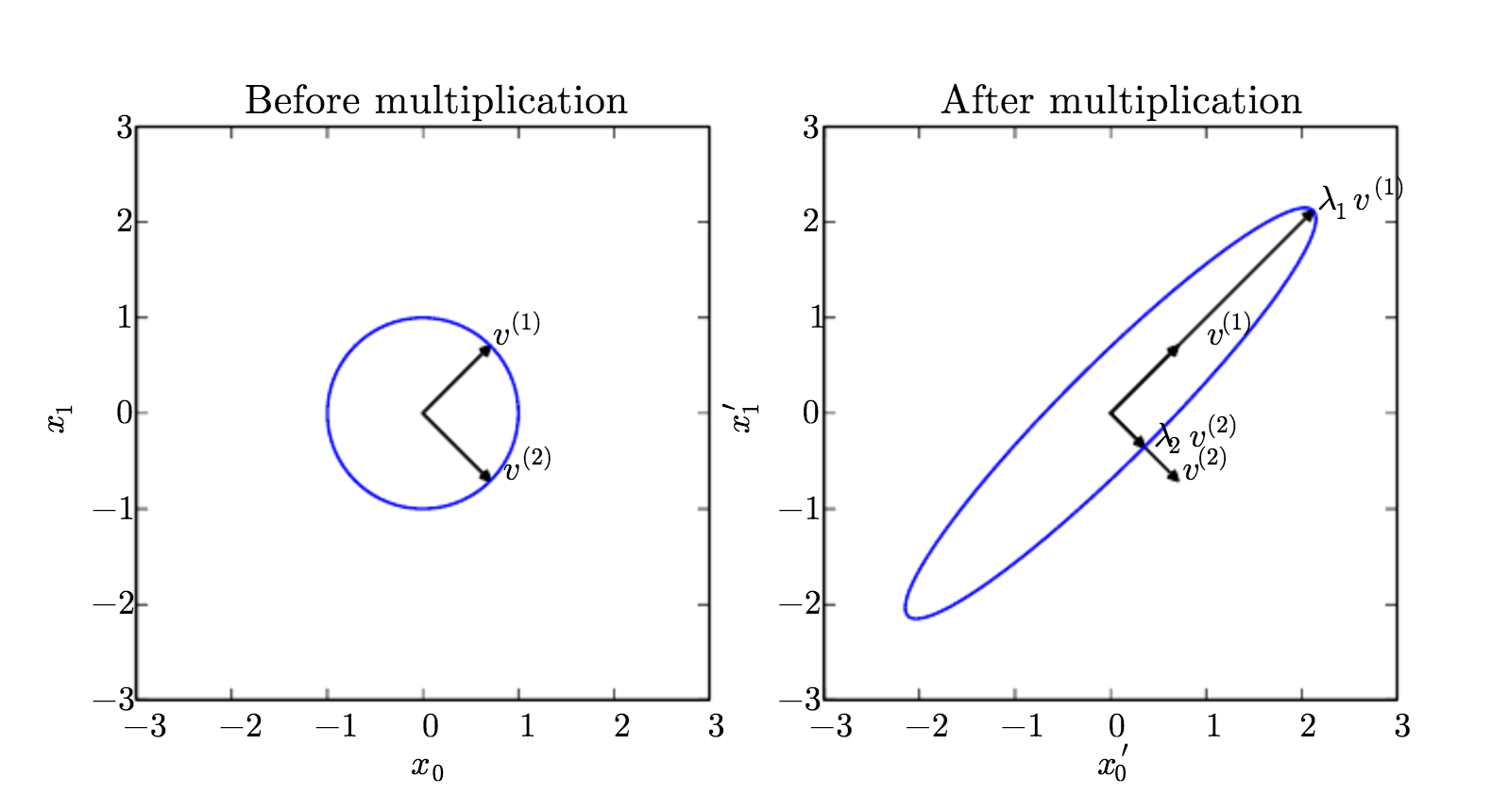
Fig 1. We have a matrix A with two orthonormal eigenvectors, v(1) with eigenvalue λ1 and v(2) with eigenvalue λ2. (Left) We plot the set of all unit vectors u ∈ R² as a unit circle. (Right) We plot the set of all points Au. By observing the way that A distorts the unit circle, we can see that it scales space in direction v(i) by λi. Image Courtesy: Deep Learning Book.চিত্র 1. আমাদের দুটি অরথনোমালাল ইগেনভেেক্টর সহ একটি ম্যাট্রিক্স এ, ভিজিও (1) ইজেনভ্যালু λ1 এবংv (2) ইজেনভ্যালু λ2 সহ রয়েছে। (Left) আমরা unit circle হিসাবে সমস্ত ইউনিট ভেক্টর ∈ R² এর সেট প্লট করি। (Right) আমরা সমস্ত পয়েন্ট Au প্ল্যাটসেট করি । যেভাবে A unit circle টিকে distorts/বিকৃত করে তা পর্যবেক্ষণ করে আমরা দেখতে পাচ্ছি যে এটি λi দ্বারা v (i) দিক দিয়ে স্থানটি স্কেল করে। চিত্র সৌজন্যে: Deep Learning Book
The eigen decomposition of a matrix tells us many useful facts about the matrix.
- The matrix is singular if and only if any of the eigenvalues are zero.
- The eigen decomposition of a real symmetric matrix can also be used to optimize quadratic expressions of the form f(x) =x´Ax subject to ||x||_2 = 1.
SINGULAR VALUE DECOMPOSITION/ ডিস্কম্পোসিশন সিঙ্গুলার ভ্যালু
একক singular value decomposition(SVD)/মান ভঙ্গ (SVD) singular vectors and singular values গুলিতে ম্যাট্রিক্সকে গুণিত করার আরেকটি উপায় সরবরাহ করে। SVD আমাদের একই ধরণের তথ্য eigen decomposition র মতো কিছু আবিষ্কার করতে দেয়। তবে SVD আরও সাধারণভাবে প্রযোজ্য। প্রতিটি আসল ম্যাট্রিক্সের একটি singular value decomposition থাকে তবে eigenvalue decomposition গুলির ক্ষেত্রে একই হয় না। উদাহরণস্বরূপ, যদি কোনও ম্যাট্রিক্স বর্গক্ষেত্র না হয় তবে eigen decomposition টি defined হয় না এবং এর পরিবর্তে আমাদের অবশ্যই singular value decomposition ব্যবহার করতে হবে।
The singular value decomposition is similar, except this time we will write A as a product of three matrices:
A = U DV´.
অনুমান করি যে, A একটি m x n ম্যাট্রিক্স।তারপরে U কে m x m ম্যাট্রিক্স হিসাবে চিহ্নিত করা হবে,D হতে হবে m × n ম্যাট্রিক্স, এবং V একটি n x n ম্যাট্রিক্স ।এই ম্যাট্রিকের প্রত্যেকটিরই একটি বিশেষ কাঠামো আছে ,ম্যাট্রিক গুলি U এবং V উভয়ই orthogonal matrices/অরথোগোনাল ম্যাট্রিক্স হতে পারে। ম্যাট্রিক্স D টি একটি diagonal matrix/তির্যক ম্যাট্রিক্স হিসাবে বিবেচিত।দ্রষ্টব্য যে D not necessarily square।D এর তির্যক বরাবর উপাদানগুলি ম্যাট্রিক্স A এর একক মান হিসাবে পরিচিত ,U কলামগুলি left-singular vectors হিসাবে পরিচিত।Vএর কলামগুলি right-singular vectors হিসাবে পরিচিত।
The Moore-Penrose Pseudoinverse
square/বর্গক্ষেত্র নয় এমন ম্যাট্রিক্সের জন্য Matrix inversion/ম্যাট্রিক্স বিপরীকরণ defined নয়। মনে করুন আমরা একটি ম্যাট্রিক্স A এর বাম-বিপরীতমুখী B তৈরি করতে চাই, যাতে আমরা একটি linear equation/রৈখিক সমীকরণ সমাধান করতে পারি:
Ax = y
by left-multiplying each side to obtain x = By.
by left-multiplying each side to obtain x = By.
যদি A এর wideপ্রশস্ত চেয়ে লম্বা হয়, তবে এই সমীকরণটির কোনও সমাধান না হওয়া সম্ভব। যদি A এর দৈর্ঘ্যের চেয়ে wide/প্রশস্ত হয় তবে একাধিক সম্ভাব্য সমাধান হতে পারে।
মুর-পেনরোজ সিউডোয়েন্টারস আমাদের এই ক্ষেত্রে কিছুটা অগ্রগতি করতে দেয়। A এর সিউডোইনভার্স একটি ম্যাট্রিক্স হিসাবে defined হয় ।
(A+) = lim(α->0)(A´A + αI)ˆ−1 A´.
সিউডোয়েন্টার গণনা করার জন্য ব্যবহারিক অ্যালগরিদমগুলি এই definition উপর ভিত্তি করে নয়, বরং সূত্রের উপর ভিত্তি করে
(A+)= V (D+)U´,
where U, D and V are the singular value decomposition of A, and the pseudoinverse D+ of a diagonal matrix D is obtained by taking the reciprocal of its non-zero elements then taking the transpose of the resulting matrix.
How it is significant ?
যখন A এর সারিগুলির চেয়ে বেশি কলাম রয়েছে, তখন সিউডোয়েন্টার ব্যবহার করে লিনিয়ার সমীকরণটি সমাধান করা সম্ভাব্য সমাধানগুলির মধ্যে একটি সরবরাহ করে। বিশেষভাবে, এটি সম্ভাব্য সমস্ত সমাধানের মধ্যে ন্যূনতম ইউক্লিডিয়ান আদর্শ || x || ² সহ x = (A +) y এর সমাধান সরবরাহ করে।
যখন A এর কলামগুলির চেয়ে বেশি সারি রয়েছে, সেখানে কোনও সমাধান হওয়া সম্ভব। এই ক্ষেত্রে, সিউডিয়োভার্স ব্যবহার করে আমাদের x প্রদান করে যার জন্য Euclidean/ইউক্লিডিয়ান আদর্শের দিক দিয়ে Ax যতটা সম্ভব Y এর কাছাকাছি! ||Ax − y||²
Update:
The Hadamard product, s⊙t
suppose s and t are two vectors of the same dimension. Then we use s⊙t to denote the elementwise product of the two vectors. Thus the components of s⊙t are just (s⊙t)j=sjtj. As an example,
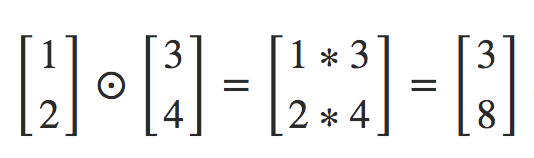
Thanks
0 comments:
Post a Comment