What is PCA?
আসুন আমরা বলি যে আপনি ভবিষ্যদ্বাণী করতে চান যে আমেরিকার gross domestic product (GDP) 2017 সালের জন্য কী হবে। আপনার কাছে প্রচুর তথ্য আছে : 2017 সালের প্রথম প্রান্তিকে মার্কিন জিডিপি, 2016,2016 সালের সম্পূর্ণতার জন্য মার্কিন জিডিপি। আপনার কাছে বেকারত্বের হার, মূল্যস্ফীতির হার ইত্যাদির মতো সর্বজনীনভাবে উপলভ্য অর্থনৈতিক সূচক রয়েছে। ২০১০ সাল থেকে আপনার কাছে মার্কিন আদমশুমারীর তথ্য আছে, প্রতিটি শিল্পে কতজন আমেরিকান কাজ করেন এবং আমেরিকান সম্প্রদায় জরিপ ডেটা প্রতিটি শুমারির মধ্যে সেই অনুমানগুলি আপডেট করে। আপনি জানেন যে হাউস এবং সিনেটের কতজন সদস্য প্রতিটি রাজনৈতিক দলের অন্তর্ভুক্ত। আপনি স্টক প্রাইসের ডেটা, এক বছরে সংঘটিত আইপিও এবং how many CEOs seem to be mounting a bid for public office. । বিবেচনার জন্য অবিচ্ছিন্ন পরিমাণে ভেরিয়েবল থাকা সত্ত্বেও, এটি কেবল পৃষ্ঠকে স্ক্র্যাচ করে ।
n.t:eigenvalue =প্রতিটি প্যারামিটারের মানগুলির একটি সেট, যার জন্য একটি ডিফারেনশিয়াল সমীকরণের দেওয়া conditions/শর্তে একটি non-zero solution (একটি আইজেনফংশন) থাকে।
টি এল; ডিআর - আপনি অনেক ভেরিয়েবল বিবেচনা করতে হবে।
আপনি যদি এর আগে অনেকগুলি ভেরিয়েবলের সাথে কাজ করে থাকেন তবে আপনি জানেন যে এটি সমস্যাগুলি উপস্থিত করতে পারে। আপনি প্রতিটি পরিবর্তনশীল মধ্যে সম্পর্ক বুঝতে পারি? আপনার কি এতগুলি ভেরিয়েবল রয়েছে যে আপনি আপনার ডেটাতে আপনার মডেলকে ফিট করার ঝুঁকিতে আছেন বা আপনি যে মডেলিং কৌশলটি ব্যবহার করছেন তা অনুমানের লঙ্ঘন করছেন?
আপনি এই প্রশ্নটি জিজ্ঞাসা করতে পারেন, "আমি যে সমস্ত পরিবর্তনশীলগুলি সংগ্রহ করেছি সেগুলি আমি কীভাবে গ্রহণ করব এবং সেগুলির মধ্যে কেবল কয়েকটিকেই ফোকাস করব?" প্রযুক্তিগত ভাষায়, আপনি "আপনার বৈশিষ্ট্যের জায়গার মাত্রা হ্রাস করতে" চান। মাত্রা হ্রাস করে আপনার বৈশিষ্ট্য স্থানটি বিবেচনা করার জন্য আপনার ভেরিয়েবলের মধ্যে কম সম্পর্ক রয়েছে এবং আপনার মডেলটি আপনার চেয়ে বেশি মানায়। (দ্রষ্টব্য: এটি অবিলম্বে এর অর্থ এই নয় যে অতিরিক্ত চাপ দেওয়া ইত্যাদি এখন আর উদ্বেগ নয় - তবে আমরা সঠিক দিকে এগিয়ে যাচ্ছি!)
কিছুটা আশ্চর্যজনকভাবে, বৈশিষ্ট্যটির জায়গার reducing the dimension/মাত্রা হ্রাস করার নামটিকে "dimensionality reduction মাত্রিকতা হ্রাস " বলা হয় dimen মাত্রিকতা হ্রাস অর্জনের অনেকগুলি উপায় রয়েছে তবে এই কৌশলগুলির বেশিরভাগই দুটি শ্রেণির একটিতে পড়ে:
- Feature Eliminationবৈশিষ্ট্য নির্মূল
- Feature Extractionবৈশিষ্ট্য নিষ্কাশন
বৈশিষ্ট্য নির্মূলকরণ এর মত যা মনে হচ্ছে: আমরা বৈশিষ্ট্যগুলি বাদ দিয়ে বৈশিষ্ট্যের স্থান হ্রাস করি। উপরের জিডিপি উদাহরণে, প্রতিটি একক ভেরিয়েবল বিবেচনার পরিবর্তে, আমরা মনে করি যে তিনটি মার্কিন যুক্তরাষ্ট্রে মোট দেশীয় পণ্য কেমন হবে তা ভালভাবে পূর্বাভাস দেওয়া বাদে সমস্ত পরিবর্তনশীল বাদ দিতে পারি। বৈশিষ্ট্য বর্জন পদ্ধতিগুলির সুবিধাগুলির মধ্যে সরলতা এবং আপনার ভেরিয়েবলগুলির ব্যাখ্যাযোগ্যতা বজায় রাখা অন্তর্ভুক্ত।
অসুবিধে হিসাবে, আপনি যে ভেরিয়েবলগুলি বাদ দিয়েছিলেন সেগুলি থেকে কোনও তথ্য আপনি পাবেন না। আমরা যদি কেবলমাত্র গত বছরের জিডিপি, অতি সাম্প্রতিক আমেরিকান কমিউনিটি জরিপ সংখ্যা অনুযায়ী উত্পাদন কর্মসংস্থানের জনসংখ্যার অনুপাত এবং এই বছরের জিডিপিকে পূর্বাভাস দিতে বেকারত্বের হার ব্যবহার করি, তবে বাদ পড়া ভেরিয়েবলগুলি আমাদের মডেলটিতে অবদান রাখতে পারে তা আমরা ভুলে যাচ্ছি না। বৈশিষ্ট্যগুলি অপসারণ করে, আমরা বাদ দেওয়া ভেরিয়েবলগুলি যে উপকারগুলি নিয়ে আসবে তা সম্পূর্ণরূপেও সরিয়ে ফেলেছি।
বৈশিষ্ট্য নিষ্কাশন , তবে, এই সমস্যার মধ্যে চলে না। বলুন আমাদের দশটি স্বাধীন ভেরিয়েবল রয়েছে। বৈশিষ্ট্য আহরণে, আমরা দশটি "নতুন" স্বতন্ত্র ভেরিয়েবল তৈরি করি, যেখানে প্রতিটি "নতুন" স্বতন্ত্র ভেরিয়েবল দশটি "পুরানো" স্বতন্ত্র ভেরিয়েবলগুলির প্রত্যেকটির সংমিশ্রণ। যাইহোক, আমরা একটি নির্দিষ্ট উপায়ে এই নতুন স্বতন্ত্র ভেরিয়েবলগুলি তৈরি করি এবং তারা আমাদের নির্ভরশীল ভেরিয়েবলের কতটা ভাল পূর্বাভাস দেয় তার দ্বারা এই নতুন ভেরিয়েবলগুলি অর্ডার করি।
আপনি হয়ত বলতে পারেন, " dimensionality reductionমাত্রিকতা হ্রাস কোথা থেকে আসে?" ভাল, আমরা যতগুলি নতুন independent variables চাই তা রাখি, তবে আমরা " least important onesগুলি" ফেলে রাখি কারণ আমরা নতুন ভেরিয়েবলগুলিকে কতটা ভালভাবে আদেশ দিয়েছিলাম , আমাদের dependent variable টির পূর্বাভাস দিন, আমরা জানি কোন পরিবর্তনশীল most important and least important তবে - এবং এখানে here’s the kicker - কারণ এই নতুন স্বতন্ত্র ভেরিয়েবলগুলি আমাদের পুরানোগুলির সংমিশ্রণ, আমরা এখনও আমাদের পুরানো ভেরিয়েবলগুলির সর্বাধিক মূল্যবান অংশ রাখছি, এমনকি যখন আমরা এই "নতুন" ভেরিয়েবলগুলির এক বা একাধিক ড্রপ করি তখনও!
Principal component বিশ্লেষণ বৈশিষ্ট্য আহরণের জন্য একটি কৌশল - সুতরাং এটি আমাদের ইনপুট ভেরিয়েবলগুলিকে একটি নির্দিষ্ট উপায়ে একত্রিত করে, তারপরেও আমরা সমস্ত ভেরিয়েবলের সর্বাধিক মূল্যবান অংশগুলি বজায় রেখে "সর্বনিম্ন গুরুত্বপূর্ণ" ভেরিয়েবলগুলি ফেলে দিতে পারি! একটি অতিরিক্ত সুবিধা হিসাবে, পিসিএর পরে প্রতিটি "নতুন" ভেরিয়েবলগুলি একে অপরের থেকে পৃথক। এটি একটি সুবিধা কারণ লিনিয়ার মডেলের অনুমানগুলির জন্য আমাদের স্বতন্ত্র ভেরিয়েবলগুলি একে অপরের থেকে স্বতন্ত্র হওয়া প্রয়োজন। যদি আমরা এই "নতুন" ভেরিয়েবলগুলির সাথে লিনিয়ার রিগ্রেশন মডেলটি ফিট করার সিদ্ধান্ত নিই (see “principal component regression” below), এই অনুমানটি অগত্যা সন্তুষ্ট হবে।
When should I use PCA?
- আপনি কি ভেরিয়েবলের সংখ্যা হ্রাস করতে চান, তবে বিবেচনা থেকে সম্পূর্ণ অপসারণ করতে ভেরিয়েবলগুলি সনাক্ত করতে সক্ষম নন?
- আপনার ভেরিয়েবলগুলি একে অপরের থেকে পৃথক কিনা তা নিশ্চিত করতে চান?
- আপনি কি আপনার স্বতন্ত্র ভেরিয়েবলগুলি কম ব্যাখ্যামূলক করে তুলতে আরামদায়ক?
আপনি যদি তিনটি প্রশ্নের উত্তর "হ্যাঁ" দিয়ে থাকেন তবে PCA ব্যবহারের জন্য একটি ভাল পদ্ধতি। যদি আপনি 3 নম্বর প্রশ্নের উত্তর "না" দিয়ে থাকেন তবে আপনার PCA ব্যবহার করা উচিত নয় ।
How does PCA work?
এর পরে বিভাগটি পিসিএ কেন কাজ করে তা আলোচনা করা হবে, তবে অ্যালগোরিদমে ঝাঁপ দেওয়ার আগে একটি সংক্ষিপ্তসার সরবরাহ করা প্রসঙ্গে সহায়ক হতে পারে:
- আমরা একটি ম্যাট্রিক্স গণনা করতে যাচ্ছি যাতে আমাদের ভ্যারিয়েবলগুলি কীভাবে একে অপরের সাথে সম্পর্কিত হয় তা সংক্ষিপ্ত করে দেয়।
- এরপরে আমরা এই ম্যাট্রিক্সকে দুটি পৃথক পৃথক অংশে বিভক্ত করব: direction and magnitude/দিক এবং প্রস্থতা। তারপরে আমরা আমাদের ডেটাগুলির "directions/দিকনির্দেশগুলি" এবং এর "magnitude/বিশালতা" (or how “important” each direction is/ প্রতিটি দিকটি কতটা "গুরুত্বপূর্ণ") তা বুঝতে পারি। নীচে স্ক্রিনশটটি সেটোসা.আইও অ্যাপলেট থেকে এই তথ্যটিতে দুটি প্রধান দিক প্রদর্শন করে: "লাল দিক" এবং "সবুজ দিক" এই ক্ষেত্রে, "লাল দিক" আরও গুরুত্বপূর্ণ। পরে কেন এটি হবে তা আমরা তা নিয়ে যাব, তবে বিন্দুগুলি কীভাবে সাজানো হয়েছে তা আপনি দেখতে পাচ্ছেন যে কেন "লাল দিক" "সবুজ দিক?" এর চেয়ে বেশি গুরুত্বপূর্ণ দেখাচ্ছে ( ইঙ্গিত: সর্বোত্তম ফিটের একটি লাইনে কী উপযুক্ত? এই তথ্য মত দেখতে? )
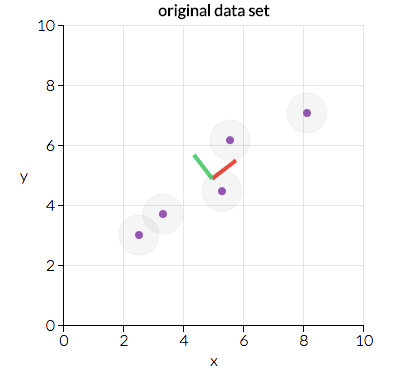
আমরা আমাদের মূল ডেটাগুলিকে এই গুরুত্বপূর্ণ দিকগুলি (যা আমাদের মূল ভেরিয়েবলগুলির সংমিশ্রণ) সাথে একত্রিত করতে রূপান্তর করব। নীচের স্ক্রিনশটটি ( আবার সেটোসা.আইও থেকে ) উপরের মতো একই তথ্য, তবে রূপান্তরিত হয়েছে যাতে x এবং y- x গুলি এখন "লাল দিক" এবং "সবুজ দিক" এখানে সেরা ফিটের লাইনটি দেখতে কেমন হবে?
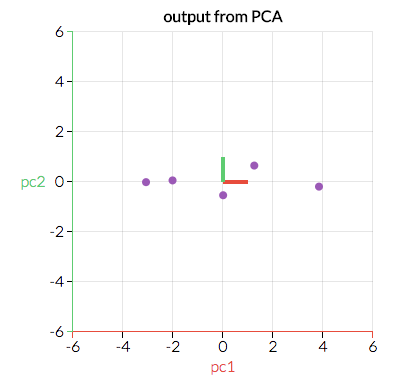
- যদিও এখানে visual example টি two-dimensional (এবং এইভাবে আমাদের two “directions" রয়েছে), এমন একটি ক্ষেত্রে চিন্তা করুন যেখানে আমাদের ডেটাটির আরও dimensions রয়েছে। চিহ্নিত করণের যেটি "dimensions গুলি" হয় সবচেয়ে কসম "important," আমরা কম্প্রেস বা একটি smaller space "দিকনির্দেশগুলিতে" যে ড্রপ দ্বারা আমাদের তথ্য প্রকল্প করতে পারি "least important।" , আমরা হ্রাস করছি একটি smaller space আমাদের তথ্য জরিপ অনুযায়ী আমাদের feature space র dimensionality… তবে, কারণ আমরা এই বিভিন্ন "directions" আমাদের ডেটা পরিবর্তন করেছি, আমরা আমাদের মডেলটিতে সমস্ত আসল ভেরিয়েবলগুলি নিশ্চিত করে রেখেছি!
এখানে, আমি PCA পরিচালনার জন্য একটি অ্যালগরিদম দিয়ে চলেছি। আমি খুব প্রযুক্তিগত না হওয়ার চেষ্টা করি, তবে এখানে বিশদটি উপেক্ষা করা অসম্ভব, তাই আমার লক্ষ্যটি যতটা সম্ভব স্পষ্টভাবে জিনিসগুলির মধ্যে দিয়ে চলা। অ্যালগরিদম কেন কাজ করে তার একটি গভীর স্বীকৃতি পরবর্তী বিভাগে উপস্থাপন করা হয়েছে।
শুরু করার আগে, আপনার n টি সারি এবং সম্ভবত p+ 1 কলামের সাথে tabular data সাজানো উচিত , যেখানে একটি কলাম আপনার নির্ভরশীল ভেরিয়েবলের সাথে মিলিত হয় (সাধারণত ডায়াটড y ) এবং p কলাম যেখানে প্রতিটি স্বindependent variable র সাথে মিলে যায় (যার ম্যাট্রিক্স সাধারণত চিহ্নিত করা হয়) x )
- যদি কোনও Y ভেরিয়েবল উপস্থিত থাকে এবং এটি আপনার ডেটার অংশ হয়, তবে উপরের সংজ্ঞায়িত হিসাবে আপনার ডেটা Y এবং X এ আলাদা করুন - আমরা বেশিরভাগ x এর সাথে কাজ করব । (দ্রষ্টব্য: যদি y র জন্য কোনও কলাম না থাকে তবে তা ঠিক আছে - পরবর্তী পয়েন্টে যান!)
- স্বাধীন ভেরিয়েবল x এর ম্যাট্রিক্স নিন এবং প্রতিটি কলামের জন্য, প্রতিটি এন্ট্রি থেকে কলামটির গড় বিয়োগ করুন। (এটি নিশ্চিত করে যে প্রতিটি কলামের শূন্যের গড় রয়েছে))
- standardize/মানীকরণ করবেন কিনা তা সিদ্ধান্ত নিন। x এর কলামগুলি দেওয়া , higher variance বৈশিষ্ট্যগুলি কি কম বৈকল্পিকের বৈশিষ্ট্যগুলির চেয়ে বেশি গুরুত্বপূর্ণ, বা বৈশিষ্ট্যের গুরুত্ব বৈকল্পিকের চেয়ে আলাদা? ( এক্ষেত্রে , গুরুত্বের অর্থ সেই বৈশিষ্ট্যটি y র পূর্বাভাসটি কতটা ভাল )) বৈশিষ্ট্যগুলির গুরুত্ব যদি বৈশিষ্ট্যের ভিন্নতার থেকে আলাদা হয়, তবে প্রতিটি পর্যবেক্ষণটি কলামের মানক বিচ্যুতির মাধ্যমে একটি কলামে ভাগ করুন। (এটি, পদক্ষেপ 2 এর সাথে মিলিত, প্রতিটি কলামের শূন্য এবং মান বিচ্যুতির পরিমাণটি নিশ্চিত করার জন্য X এর প্রতিটি কলামকে মানিক করে তোলে)) কেন্দ্রিক (এবং সম্ভবত মানকযুক্ত) ম্যাট্রিক্স z কল করে ।
- ম্যাট্রিক্স z নিন , transpose itএটিকে স্থানান্তর করুন এবং ট্রান্সপোজড ম্যাট্রিক্সকে z দ্বারা গুণ করুন । (গাণিতিকভাবে এটি লেখার জন্য, আমরা এটি zᵀ z হিসাবে লিখব ।) ফলস্বরূপ ম্যাট্রিক্সটি ধ্রুবক অবধি covariance matrix of Z,
- (এটি সম্ভবত কঠিন পদক্ষেপ অনুসরণ করতে হয়এখানে , Calculate the eigenvectors and their corresponding eigenvalues of ZᵀZ.। এটি পুরোপুরি সহজে আসলে সবচেয়ে কম্পিউটিং packages- মধ্যে সম্পন্ন করা হয়, eigendecomposition এর z ᵀ z যেখানে আমরা decompose ZᵀZ into PDP⁻¹ , যেখানে p eigenvectors ম্যাট্রিক্স এবং D তির্যক এবং এর eigenvalues সঙ্গে তির্যক ম্যাট্রিক্স হয় অন্য কোথাও শূন্যের মান। D এর তির্যকটি সম্পর্কিত ইগেনভ্যালুগুলি p -তে সংশ্লিষ্ট কলামের সাথে যুক্ত হবে - যা D এর প্রথম উপাদান D is λ₁ এবং সংশ্লিষ্ট eigenvector টি p এর প্রথম কলাম। এটি D এর সমস্ত উপাদানএবং p তে তাদের সম্পর্কিত ইগেনভেেক্টরকে ধারণ করে। আমরা সর্বদাএই ফ্যাশনে PDP গণনা করতে সক্ষম হব। (বোনাস: আগ্রহীদের জন্য, আমরা সবসময় পিডিপি -কে এই ফ্যাশনে গণনা করতে পারি কারণ, zᵀ z একটি symmetric, positive semidefinite matrix./প্রতিসাম্য , ইতিবাচক অর্ধবৃত্তিমূলক ম্যাট্রিক্স )
- eigenvalues গুলি λ₁, λ₂, …, λp নিন এবং এটিকে বৃহত্তম থেকে ক্ষুদ্রতম পর্যন্ত বাছাই করুন। এটি করার মাধ্যমে, p অনুসারে eigenvectors গুলিকে বাছাই করুন । (উদাহরণস্বরূপ, যদি λ₂ বৃহত্তম ইগেনভ্যালু হয় তবে p এর দ্বিতীয় কলামটি নিয়ে এটি প্রথম কলামের অবস্থানে রাখুন)) কম্পিউটিং প্যাকেজের উপর নির্ভর করে এটি স্বয়ংক্রিয়ভাবে সম্পন্ন হতে পারে। eigenvectors P * এর এই সাজানো ম্যাট্রিক্সকে কল করুন । ( p * এর কলামগুলি p এর কলামগুলির মতো হওয়া উচিত , তবে সম্ভবত অন্য কোনও ক্রমে।) নোট করুন যে এই আইজেনভেেক্টরগুলি একে অপরের থেকে স্বতন্ত্র।
- z * = zp * গণনা করুন । এই নতুন ম্যাট্রিক্স, z* , x এর কেন্দ্রিক / মানকৃত সংস্করণ তবে এখন প্রতিটি পর্যবেক্ষণটি মূল ভেরিয়েবলগুলির সংমিশ্রণ, যেখানে ওজনগুলি ইগেনভেেক্টর দ্বারা নির্ধারিত হয়। বোনাস হিসাবে, যেহেতু p* তে আমাদের ইগেনভেেক্টর একে অপরের থেকে পৃথক, z * এর প্রতিটি কলামও একে অপরের থেকে পৃথক!
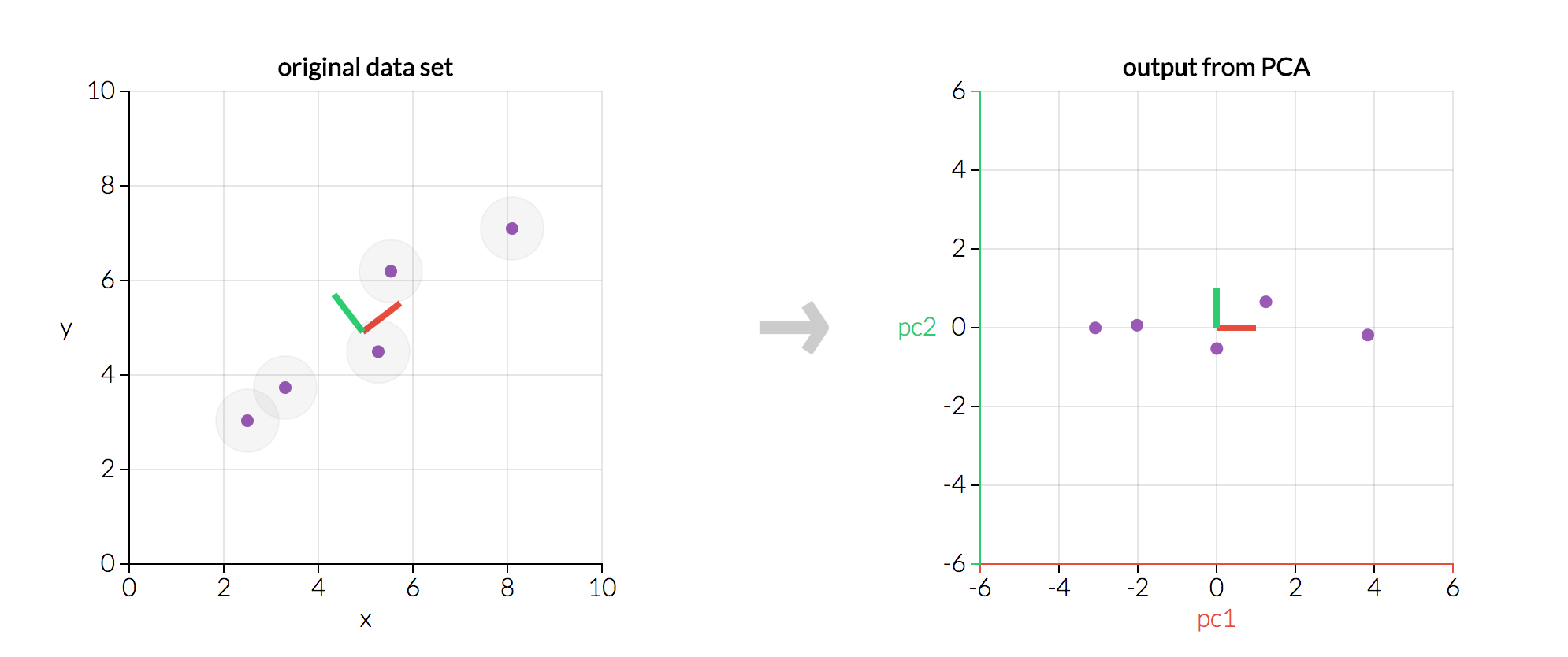
An example from setosa.io where we transform five data points using PCA. The left graph is our original data X; the right graph would be our transformed data Z*.
এই গ্রাফিকের দুটি জিনিস নোট করুন:
- দুটি চার্ট হুবহু একই ডেটা দেখায়, তবে ডান গ্রাফটি মূল ডেটাটি রূপান্তরিত করে যাতে আমাদের অক্ষগুলি এখন মূল উপাদান।
- উভয় গ্রাফের মধ্যে মূল উপাদানগুলি একে অপরের লম্ব হয়। প্রকৃতপক্ষে, প্রতিটি প্রধান উপাদান সর্বদা প্রতিটি অন্যান্য মূল উপাদানগুলির জন্য orthogonal অ্যাপলেটটি ভেঙে দেওয়ার চেষ্টা করুন !)
যেহেতু আমাদের প্রধান উপাদানগুলি একে অপরের কাছে অর্থেগোনাল, তারা পরিসংখ্যানগতভাবে একে অপরের থেকে রৈখিকভাবে স্বাধীন ... যার কারণে আমাদের z* এর কলামগুলি একে অপরের থেকে রৈখিকভাবে স্বাধীন!
৮. অবশেষে, আমাদের নির্ধারণ করতে হবে যে কতগুলি বৈশিষ্ট্য বর্জন করতে হবে তার বিপরীতে রাখতে হবে। এটি নির্ধারণের জন্য তিনটি সাধারণ পদ্ধতি রয়েছে, নীচে আলোচনা করা হয়েছে এবং এর পরে একটি স্পষ্ট উদাহরণ রয়েছে:
- পদ্ধতি 1 : আমরা কয়টি মাত্রা রাখতে চাই তা নির্বিচারে নির্বাচন করি সম্ভবত আমি জিনিসগুলিকে দুটি মাত্রায় দৃশ্যত উপস্থাপন করতে চাই, তাই আমি কেবল দুটি বৈশিষ্ট্য রাখতে পারি। এটি ব্যবহারের ক্ষেত্রে নির্ভরশীল এবং আমার কতগুলি বৈশিষ্ট্য বাছাই করা উচিত তার পক্ষে কোনও hard-and-fast rule নিয়ম নেই।
- পদ্ধতি 2 : প্রতিটি বৈশিষ্ট্যের জন্য ব্যাখ্যা করা (নীচে সংক্ষিপ্তভাবে ব্যাখ্যা করা হয়েছে) এর অনুপাতের গণনা কর , একটি threshold চয়ন কর এবং যতক্ষণ না আপনি সেই প্রান্তে আঘাত না করেন ততক্ষণ বৈশিষ্ট্য যুক্ত করুন। (উদাহরণস্বরূপ, আপনি যদি আপনার মডেলের দ্বারা বর্ণিত মোট চলকটির ৮০% ব্যাখ্যা করতে চান তবে আপনার বৈকল্পিকের অনুপাত হিট 80% ছাড়িয়ে না যাওয়া পর্যন্ত তারতম্যের বৃহত্তম ব্যাখ্যাযোগ্য অনুপাত সহ বৈশিষ্ট্যগুলি যুক্ত করুন)
- পদ্ধতি 3 : এটি 2 পদ্ধতির সাথে ঘনিষ্ঠভাবে সম্পর্কিত প্রতিটি বৈশিষ্ট্যের জন্য ব্যাখ্যা করা বৈকল্পিকের অনুপাতের গণনা করুন , বিভিন্ন বৈশিষ্ট্যের অনুপাত অনুসারে বৈশিষ্ট্যগুলি সাজান এবং আপনি আরও বৈশিষ্ট্য রাখার কারণে পরিবর্তনের সংখ্যামূলক অনুপাত ব্যাখ্যা করেছেন (এই প্লটটিকে একটিscree plot বলা হয় , নীচে দেখানো হয়েছে) নতুন বৈশিষ্ট্য যুক্ত করার সাথে পূর্ববর্তী বৈশিষ্ট্যের তুলনায় বিশদরূপে উল্লেখযোগ্য হ্রাস পাওয়া যায় এবং সেই বিন্দু অবধি বৈশিষ্ট্যগুলি বেছে নিয়ে পয়েন্ট চিহ্নিত করে কতগুলি বৈশিষ্ট্য অন্তর্ভুক্ত করা যায় তা বেছে নিতে পারে । (আমি এটিকে "find the elbow" পদ্ধতি বলি, যেমন স্ক্রি প্লটের "bend” or “elbow" দেখলে নির্ধারিত হয় যে proportion অনুপাতের biggest drop টি কোথায় ঘটে))
যেহেতু প্রতিটি ইগেনভ্যালু মোটামুটি তার সম্পর্কিত eigenvalue টির গুরুত্ব, তাই পরিবর্তিততার অনুপাতের বিবরণ হ'ল সমস্ত বৈশিষ্ট্যের ইগনাল্যুজের যোগফল দ্বারা আপনি যে বৈশিষ্ট্যগুলিকে বিভক্ত রেখেছেন সেগুলির ইউজভ্যালুগুলির যোগফল।
জেনেটিক ডেটার জন্য এই স্ক্রি প্লটটি বিবেচনা করুন। (উত্স: এখানে ।) লাল রেখাটি প্রতিটি বৈশিষ্ট্য দ্বারা ব্যাখ্যা করা বৈকল্পিকের অনুপাত নির্দেশ করে, যা মূল উপাদানটির eigenvalue গুলি সমস্ত eigenvalue র সমষ্টি দ্বারা বিভক্ত করে গণনা করা হয়। কেবলমাত্র মূল উপাদান 1 যুক্ত করে ব্যাখ্যা করা proportion of variance হ'ল λ₁ / (λ₁ + λ₂ +… + λ পি ), যা প্রায় 23%। কেবলমাত্র প্রধান উপাদান 2 অন্তর্ভুক্ত করে ব্যাখ্যা করা proportion of variance হ'ল λ₂ / (λ₁ + λ₂ +… + λ পি ), বা প্রায় 19%।
মূল উপাদান 1 এবং 2 উভয়কে ব্যাখ্যা করে find the elbow হ'ল (λ₁ + λ₂) / (λ₁ + λ₂ +… + λ পি ), যা প্রায় ৪২%। এখানেই হলুদ রেখা আসে; হলুদ রেখাটি ব্যাখ্যা করে যে সংখ্যার বিস্তৃত পরিমাণের সংক্ষিপ্ত পরিমাণটি আপনি যদি সেই বিন্দু পর্যন্ত সমস্ত মূল উপাদান অন্তর্ভুক্ত করেন explained উদাহরণস্বরূপ, পিসি 2 এর ওপরে হলুদ বিন্দুটি নির্দেশ করে যে প্রধান 1 এবং 2 টি সহ মডেলটির মোট proportion র প্রায় 42% ব্যাখ্যা করবে।
এখন কয়েকটি উদাহরণ দেওয়া যাক:
- পদ্ধতি 1: আমরা সম্মিলিতভাবে অন্তর্ভুক্ত করার জন্য অনেকগুলি মূল উপাদান নির্বাচন করি। ধরুন আমি আমার মডেলটিতে পাঁচটি মূল উপাদান রাখতে চেয়েছিলাম। উপরের জেনেটিক ডেটা ক্ষেত্রে, এই পাঁচটি মূল উপাদানগুলি মোট 13 টি মূল উপাদানকে অন্তর্ভুক্ত করে মোট চলকের প্রায় 66% ব্যাখ্যা করবে।
- পদ্ধতি 2: ধরুন আমি 13 টি প্রধান উপাদান দ্বারা বর্ণিত মোট পরিবর্তনশীলতার 90% ব্যাখ্যা করার জন্য পর্যাপ্ত মূল উপাদানগুলি অন্তর্ভুক্ত করতে চেয়েছিলাম। উপরের জেনেটিক ডেটা ক্ষেত্রে, আমি প্রথম 10 প্রধান উপাদান অন্তর্ভুক্ত করব এবং Z * থেকে চূড়ান্ত তিনটি ভেরিয়েবলগুলি ফেলে দেব ।
- পদ্ধতি 3: এখানে, আমরা "find the elbow" চাই উপরের স্ক্রি প্লটে আমরা দেখতে পেলাম মূল উপাদান 2 এবং প্রধান উপাদান 3 এর মধ্যে ব্যাখ্যাযোগ্য find the elbow র একটি বড় হ্রাস , এই ক্ষেত্রে, আমরা সম্ভবত অন্তর্ভুক্ত করব প্রথম দুটি বৈশিষ্ট্য এবং বাকি বৈশিষ্ট্যগুলি বাদ দিন। আপনি দেখতে পাচ্ছেন যে, এই পদ্ধতিটি কিছুটা বিষয়গত কারণ "elbow" এর গাণিতিকভাবে সঠিক সংজ্ঞা নেই এবং এক্ষেত্রে আমরা এমন একটি মডেল অন্তর্ভুক্ত করব যা মোট চলকের মাত্র প্রায় 42% ব্যাখ্যা করে।
(দ্রষ্টব্য: কিছু স্ক্রি প্লটের মধ্যে বৈকল্পিকের অনুপাতের চেয়ে Y অক্ষের উপরে ইগেনভেক্টরগুলির আকার থাকবে , এটি সমপরিমাণ ফলাফলের দিকে পরিচালিত করে, তবে ব্যবহারকারীকে ম্যানুয়ালি তারতম্যের অনুপাত গণনা করতে হবে ,এর উদাহরণ এখানে দেখা যায় । )
একবার আমরা যে রূপান্তরিত ভেরিয়েবলগুলি বাদ দিতে চাইছি তা বাদ দিলে আমরা শেষ হয়ে গেলাম! এটি PCA।
Once we’ve dropped the transformed variables we want to drop, we’re done! That’s PCA.
PCA কেন কাজ করে?
যদিও PCA একটি গভীর প্রযুক্তিগত পদ্ধতিতে, লিনিয়ার বীজগণিত অ্যালগোরিদমগুলির উপর নির্ভর করে, আপনি যখন এটি সম্পর্কে চিন্তা করেন এটি তুলনামূলক intuitive method/স্বজ্ঞাত পদ্ধতি।
- প্রথমত, সহভেদাংক ম্যাট্রিক্স z ᵀ z একটি ম্যাট্রিক্স যে কিভাবে প্রতিটি পরিবর্তনশীল আনুমানিক পরিসংখ্যান রয়েছে z প্রতিটি অন্যান্য পরিবর্তনশীল সম্পর্কিত z । কীভাবে একটি ভেরিয়েবল অন্যটির সাথে যুক্ত তা বোঝা বেশ শক্তিশালী।
- দ্বিতীয়ত, eigenvalue গুলি এবং eigenvalue গুলি গুরুত্বপূর্ণ। eigenvalue নির্দেশাবলী উপস্থাপন করে। একটি বহুমাত্রিক scatterplot আপনার ডেটা প্লট করার কথা ভাবুন। তারপরে কেউ আপনার ডেটার scatterplot একটি পৃথক eigenvalue কে একটি নির্দিষ্ট "দিকনির্দেশনা" হিসাবে ভাবতে পারে। eigenvalue গুলি আকার বা গুরুত্বকে উপস্থাপন করে। আরও বড় দিকনির্দেশগুলি আরও গুরুত্বপূর্ণ দিকের সাথে সম্পর্কিত।
- পরিশেষে, আমরা একটি অনুমান করি যে একটি নির্দিষ্ট দিকের আরও পরিবর্তনশীলতার সাথে নির্ভরশীল ভেরিয়েবলের আচরণ ব্যাখ্যা করার সাথে সম্পর্কিত হয়। প্রচুর পরিবর্তনশীলতা সাধারণত সংকেতকে নির্দেশ করে তবে সামান্য পরিবর্তনশীলতা সাধারণত শব্দকে নির্দেশ করে। সুতরাং, নির্দিষ্ট দিকটিতে যত বেশি পরিবর্তনশীলতা রয়েছে তাত্ত্বিকভাবে, আমরা সনাক্ত করতে চাই এমন কোনও গুরুত্বপূর্ণ বিষয়টির সূচক। (The setosa.io PCA applet সেটোসা.ইও পিসিএ অ্যাপলেটটি ডেটা নিয়ে ঘুরে দেখার এক দুর্দান্ত উপায় এবং কেন তা বোঝায় তা নিজেকে বোঝান)
সুতরাং, পিসিএ একটি পদ্ধতি যা একত্রিত করে:
- প্রতিটি পরিবর্তনশীল একে অপরের সাথে কীভাবে যুক্ত তার একটি পরিমাপ। (Covariance matrix/সহভেদাংক ম্যাট্রিক্স)
- যে সমস্ত দিকগুলিতে আমাদের ডেটা ছড়িয়ে দেওয়া হয় (Eigenvectors)
- এই বিভিন্ন দিকের আপেক্ষিক গুরুত্ব। (Eigenvalues।)
PCA আমাদের predictor র একত্রিত করে এবং আমাদের তুলনামূলকভাবে গুরুত্বহীন ইগেনভেক্টরগুলি ফেলে দেওয়ার অনুমতি দেয়।
PCA র কি এক্সটেনশন আছে?
হ্যাঁ, আমি এখানে যুক্তিসঙ্গত পরিমাণে ঠিকানার চেয়ে আরও বেশি কিছু করতে পারি। যা আমি প্রায়শই দেখেছি তা হ'ল মূল উপাদানগুলির রিগ্রেশন , যেখানে আমরা আমাদের অপরিকল্পিত yনিয়ে থাকি এবং z * এর সাবসেটে এটি ফেলে রাখি যা আমরা ছাড়িনি। (এইখানেই z * এর কলামগুলির স্বতন্ত্রতা আসে; z * -এ ওয়াইকে পুনরায় চাপিয়ে দিয়ে আমরা জানি যে স্বাধীন ভেরিয়েবলগুলির প্রয়োজনীয় স্বাধীনতা প্রয়োজনীয়ভাবে সন্তুষ্ট হবে However আমাদের অন্যান্য অনুমানগুলি এখনও আমাদের পরীক্ষা করা দরকার)
অন্যান্য যে সমস্ত সাধারণ দেখা যায় সেগুলি হ'ল কার্নেল পিসিএ kernel PCA.।
উপসংহার
আমি আশা করি আপনি এই নিবন্ধটি সহায়ক খুঁজে পেয়েছি! PCA আরও গভীর-আলোচনার জন্য নীচের কিছু সংস্থানগুলি দেখুন। আপনি কী ভাবেন তা আমাকে জানান, বিশেষত উন্নতির জন্য যদি কোনও পরামর্শ থাকে।
আমাকে বলা হয়েছে যে এই নিবন্ধটির একটি চীনা অনুবাদ এখানে উপলব্ধ করা হয়েছে । (ধন্যবাদ, জাকুকিও ফ্রিল !)
আমি PCA র চাক্ষুষ ও স্বজ্ঞাত প্রদর্শনের জন্য সেটোসা.আইপি অ্যাপলেটকে একটি বিশাল এইচটি / টি দিতে চাই ।
সম্পাদনা করুন: উপরের Step ধাপে Z * এর সূত্রে টাইপো লক্ষ্য করার জন্য মাইকেল ম্যাথিউজকে ধন্যবাদ । তিনি সঠিকভাবে নির্দেশ করেছেন যে Z * = ZP * , Z ᵀ P * নয় । উপরের আট ধাপে অন্য টাইপো লক্ষ্য করার জন্য চিয়েনলুং চেউংকেও ধন্যবাদ জানানো হয়েছে, এবং আমি উল্লেখ করেছি যে আমি "ইগেনভেক্টর" কে একটি লাইনে "ইগেনভ্যালু" দিয়ে সংযুক্ত করেছি।
Resources You Should Check Out:
এটি এই PCA নিবন্ধটি সংকলন করতে ব্যবহৃত সম্পদের একটি তালিকা এবং সেইসাথে PCA বোঝার জন্য আমি সাধারণত সহায়ক বলে মনে করেছি এমন অন্যান্য সংস্থানগুলি। যদি আপনি এই তালিকায় ভাল অন্তর্ভুক্ত হতে পারে এমন কোনও সংস্থান সম্পর্কে জানেন তবে দয়া করে একটি মন্তব্য দিন এবং আমি সেগুলি যুক্ত করব।
Non-Academic Articles and Resources
- সেটোসা.ওয়ের পিসিএ অ্যাপলেট । (একটি অ্যাপলেট যা আপনাকে মূল উপাদানগুলি কী এবং আপনার ডেটা মূল উপাদানগুলিকে কীভাবে প্রভাবিত করে তা কল্পনা করতে দেয়)
- পিসিএ অ্যালগরিদম এবং আলগোরিদিম নিজেই ব্লক ভবনের আধা একাডেমিক, walkthrough ।
- এই স্ট্যাক এক্সচেঞ্জ প্রশ্নের প্রথম উত্তরটি এক কথায়, বকেয়া।
- পিসিএ-তে প্যারামেট্রিক অনুমান রয়েছে কিনা তা নিয়ে আলোচনা করা একটি ক্রসভিলেটেড প্রশ্ন এবং উত্তর। (স্পোলার সতর্কতা: পিসিএ নিজেই একটি ননপ্যারামেট্রিক পদ্ধতি, তবে পিসিএ ব্যবহারের পরে রিগ্রেশন বা হাইপোথিসিস পরীক্ষার জন্য প্যারামেট্রিক অনুমানের প্রয়োজন হতে পারে))
- কোনও রিসোর্সের তালিকা উইকিপিডিয়া লিংক ছাড়া খুব কমই পূর্ণ হবে , তাই না? (উইকিপিডিয়ায় কম ঝুলন্ত ফল হওয়া সত্ত্বেও, এটি পৃষ্ঠার নীচে অতিরিক্ত লিঙ্ক এবং সংস্থানগুলির একটি শক্তিশালী তালিকা রয়েছে))
Coding Resources
- স্কেলার্ন লাইব্রেরির মধ্যে পিসিএর জন্য পাইথন ডকুমেন্টেশন । (এই লিঙ্কে উদাহরণ রয়েছে!)
- অ্যানালিটিক্স বিদ্যায় পিসিএ ব্যাখ্যা । (এই লিঙ্কে পাইথন এবং আর অন্তর্ভুক্ত রয়েছে)
- কয়েকটি শীতল প্লট দিয়ে পাইথনে পিসিএ প্রয়োগ করছে ।
- আর-তে পিসিএ বাস্তবায়নের পদ্ধতির তুলনা ।
একাডেমিক পাঠ্যপুস্তক এবং নিবন্ধ
- জেমস, উইটেন, হাস্টি এবং তিবশিরানী দ্বারা Stat মুদ্রণ পরিসংখ্যান শিক্ষার পরিচিতি । (পিসিএ 6.৩, 6.. 6. এবং ১০.২ অধ্যায়ে ব্যাপকভাবে কভার করা হয়েছে। এই বইটি লিনিয়ার রিগ্রেশন সম্পর্কিত জ্ঞান ধরেছে তবে সমস্ত বিষয় বিবেচনা করা বেশ সহজলভ্য।)
- Notes from Penn State’s STAT 505/পেন স্টেটের স্ট্যাট 505 (ফলিত মাল্টিভারিয়ট স্ট্যাটিস্টিকাল অ্যানালাইসিস) কোর্স থেকে প্রাপ্ত নোটগুলি । (আমি পেন স্টেটের অনলাইন পরিসংখ্যান কোর্সের নোটগুলি অবিশ্বাস্য বলে মনে করেছি এবং এখানে PCA বিভাগটি বিশেষভাবে সহায়ক)
- লিনিয়ার বীজগণিত এবং এর অ্যাপ্লিকেশন , 4 র্থ সংস্করণ, ডেভিড লে দ্বারা রচিত। (পিসিএ 7.৫ অধ্যায়ে আচ্ছাদিত রয়েছে।)
- গুগল রিসার্চ এ জনাথন শ্লেন্সের অধ্যক্ষ উপাদান উপাদান বিশ্লেষণ সম্পর্কিত টিউটোরিয়াল ।
- কার্নেগি মেলন বিশ্ববিদ্যালয়ের কসমা শালিজির প্রিন্সিপাল কম্পোনেন্ট বিশ্লেষণের একটি খসড়া অধ্যায় ।
- ফলিত ভবিষ্যদ্বাণীমূলক মডেলিন জি থেকে ডেটা প্রিপ্রোসেসিংয়ের ডেটার একটি অধ্যায়ে বিভাগ 3.3-তে মূল উপাদান বিশ্লেষণের (ভিজ্যুয়াল সহ!) প্রাথমিক ভূমিকা অন্তর্ভুক্ত করা হয়েছে। (এইচ সুপারিশের জন্য জে লুকাসের প্রতি ঘন্টা / টি )
- হাস্টি, তিবশিরানী এবং ফ্রেডম্যানের 10 ম মুদ্রণ পরিসংখ্যানগত শিক্ষার উপাদানসমূহ । (পিসিএ, অধ্যায় 3.5 ব্যাপকভাবে আচ্ছাদিত করা হয় 14.5 এবং 18.6। এই বই রৈখিক প্রত্যাবৃত্তি, ম্যাট্রিক্স বীজগণিত, এবং ক্যালকুলাস জ্ঞান অনুমান এবং উল্লেখযোগ্যভাবে চেয়ে বেশি প্রযুক্তিগত হয় পরিসংখ্যানগত শেখার ভূমিকা , কিন্তু দুই একটি অনুরূপ গঠন অনুসরণ সাধারণ লেখক দেওয়া ।)
স্পর্শকাতর সম্পদ
- লিনিয়ার বীজগণিত ইউটিউব সিরিজের সারমর্ম ( আইগেনভেেক্টর এবং ইগেনভ্যালুতে একটি ভিডিও সহ)এটি পিসিএ সম্পর্কিত বিশেষভাবে প্রাসঙ্গিক; এই অবিশ্বাস্য সংস্থান সম্পর্কে আমাকে সচেতন করার জন্য টিম বুক এ h / t
0 comments:
Post a Comment