এটি ডিপ লার্নিং এবং নিউরাল নেটওয়ার্কগুলির একটি শিক্ষানবিশ গাইড। নিম্নলিখিত নিবন্ধে, আমরা ডিপ লার্নিং এবং নিউরাল নেটওয়ার্কগুলির অর্থ নিয়ে আলোচনা করতে যাচ্ছি। বিশেষত, আমরা ডিপ লার্নিং অনুশীলনে কীভাবে কাজ করে তার উপর ফোকাস করব।

আপনি কি কখনও ভেবে দেখেছেন যে Google’s translator App গুগলের অনুবাদক অ্যাপ্লিকেশন কীভাবে পুরো অনুচ্ছেদগুলিকে এক মিনিট থেকে অন্য ভাষায় অনুবাদ করতে সক্ষম হয়? নেটফ্লিক্স এবং Netflix and YouTube ইউটিউব কীভাবে সিনেমা বা ভিডিওতে আমাদের স্বাদ বের করতে এবং আমাদের উপযুক্ত প্রস্তাবনা দিতে সক্ষম? অথবা কীভাবে স্ব-ড্রাইভিং গাড়িগুলি সম্ভব?

এগুলি সবই ডিপ লার্নিং এবং কৃত্রিম নিউরাল নেটওয়ার্কগুলির একটি পণ্য। ডিপ লার্নিং এবং নিউরাল নেটওয়ার্কগুলির সংজ্ঞাটি নিম্নলিখিতটিতে সম্বোধন করা হবে। আমাদের প্রথমে ডিপ লার্নিং দিয়ে শুরু করতে দেয়।

1. ডিপ লার্নিং আসলে কী?

ডিপ লার্নিং মেশিন লার্নিংয়ের একটি উপসেট যা অন্যদিকে কৃত্রিম বুদ্ধিমত্তার একটি উপসেট। কৃত্রিম বুদ্ধিমত্তা একটি সাধারণ শব্দ যা এমন কৌশলগুলিকে বোঝায় যা কম্পিউটারগুলি মানুষের আচরণের অনুকরণে সক্ষম করে। মেশিন লার্নিং ডেটাগুলিতে প্রশিক্ষিত অ্যালগরিদমগুলির একটি সেট উপস্থাপন করে যা এই সমস্তকে সম্ভব করে তোলে।

অন্যদিকে ডিপ লার্নিং হ'ল এক ধরণের মেশিন লার্নিং যা মানুষের মস্তিষ্কের কাঠামো দ্বারা অনুপ্রাণিত হয়। ডিপ লার্নিংয়ের ক্ষেত্রে এই কাঠামোটিকে একটি কৃত্রিম নিউরাল নেটওয়ার্ক বলা হয়। (ডিপ লার্নিং, মেশিন লার্নিং এবং AI য়ের মধ্যে পার্থক্যের আরও বিশদ ব্যাখ্যার জন্য দয়া করে এই ব্লগ নিবন্ধটি উল্লেখ করা । 

নিউরাল নেটওয়ার্কগুলি অ্যালগরিদমের একটি সেট যা ডেটাতে নিদর্শনগুলি সনাক্ত করতে ডিজাইন করা হয়েছে। তারা এক ধরণের মেশিন উপলব্ধি, লেবেলিং বা ক্লাস্টারিং কাঁচা ইনপুট মাধ্যমে সংবেদনশীল ডেটা ব্যাখ্যা করে। নিউরাল নেটওয়ার্কগুলির দ্বারা The patterns that are recognized by neural networks are numeric, contained in vectors, into which all real-world data, like text, time series, images or sound must be translated.

নিউরাল নেটওয়ার্কগুলি ক্লাস্টারিং, শ্রেণিবদ্ধকরণ বা রিগ্রেশনের মতো অনেক কাজ সম্পাদন করতে আমাদের সক্ষম করে। নিউরাল নেটওয়ার্কগুলির সাহায্যে আমরা এই ডেটাতে নমুনাগুলির মধ্যে সাদৃশ্য অনুযায়ী লেবেলযুক্ত ডেটাগুলি গোষ্ঠীভুক্ত বা সাজিয়ে তুলতে পারি। বা শ্রেণিবদ্ধকরণের ক্ষেত্রে, আমরা এই ডেটাসেটের নমুনাগুলিকে বিভিন্ন বিভাগে শ্রেণিবদ্ধ করার জন্য একটি লেবেলযুক্ত ডেটা সেট  নেটওয়ার্কটি প্রশিক্ষণ দিতে পারি।

আসুন আমরা একটি শ্রেণিবিন্যাসের উদাহরণটি একবার দেখে নিই এবং দেখুন যে কোনও মেশিন লার্নিং মডেল কীভাবে গভীর শেখার মডেলের তুলনায় এই কাজটি পরিচালনা করবে। অনুমান করুন যে আমরা একটি অ্যালগোরিদমিক মডেল তৈরি করেছি যা হস্তাক্ষর সংখ্যার চিত্রগুলির মধ্যে পার্থক্য করতে পারে। বা অন্য কথায়: যা একটি হাতের লিখিত সংখ্যা 0-9 বিভাগে শ্রেণিবদ্ধ করতে পারে:

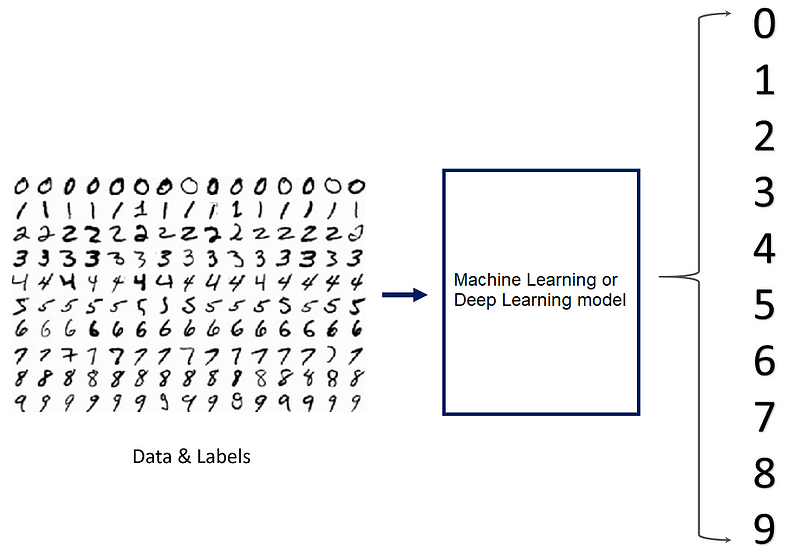
যদি আমরা একটি মেশিন লার্নিং মডেল ব্যবহার করি, তবে মডেলটিকে এমন বৈশিষ্ট্যগুলি বলা দরকার যার উপরে সংখ্যাগুলি পৃথক করা যায়। এই বৈশিষ্ট্যগুলি কোনও নির্দিষ্ট সংখ্যার আকারের উদাহরণগুলির জন্য হতে পারে। অন্যদিকে ডিপ লার্নিংয়ের সাথে বৈশিষ্ট্যগুলি নিউরাল নেটওয়ার্ক দ্বারা শিখেছে - মানুষের হস্তক্ষেপ ছাড়াই।

এই জাতীয় স্বাধীনতা অর্জনের জন্য নিউরাল নেটওয়ার্কগুলি সাধারণত মেশিন লার্নিং অ্যালগরিদমগুলির চেয়ে অনেক বেশি ডেটা প্রয়োজন। তবে, মেশিন লার্নিংয়ের মাধ্যমে নিউরাল নেটওয়ার্কগুলির আর একটি বড় সুবিধা হ'ল নিউরাল নেটওয়ার্কগুলি তাদের মেশিন লার্নিং সহযোগীদের তুলনায় অনেক ভাল পারফরম্যান্স অর্জন করতে পারে।

2. Biological Neural Networks

কৃত্রিম নিউরাল নেটওয়ার্কগুলির সাথে আর কোনও পদক্ষেপ নেওয়ার আগে আমি জৈবিক স্নায়ুবিক নেটওয়ার্কগুলির পিছনে ধারণাটি প্রবর্তন করতে চাই, সুতরাং আমরা পরে যখন কৃত্রিম নিউরাল নেটওয়ার্ককে আরও বিশদে আলোচনা করব তখন আমরা জৈবিক মডেলের সমান্তরাল দেখতে পাব।

কৃত্রিম নিউরাল নেটওয়ার্কগুলি আমাদের মস্তিস্কে পাওয়া জৈবিক নিউরনগুলি দ্বারা অনুপ্রাণিত হয়। আসলে, কৃত্রিম নিউরাল নেটওয়ার্কগুলি আমাদের মস্তিষ্কের নিউরাল নেটওয়ার্কগুলির কয়েকটি বুনিয়াদি কার্যকারিতা অনুকরণ করে তবে খুব সরল ভাবে। আসুন কৃত্রিম স্নায়ুবিক নেটওয়ার্কগুলির সাথে সমান্তরালতা পেতে জৈবিক নিউরাল নেটওয়ার্কগুলিতে প্রথমে নজর দেওয়া যাক। সংক্ষেপে, একটি জৈবিক নিউরাল নেটওয়ার্ক অসংখ্য নিউরন নিয়ে গঠিত।

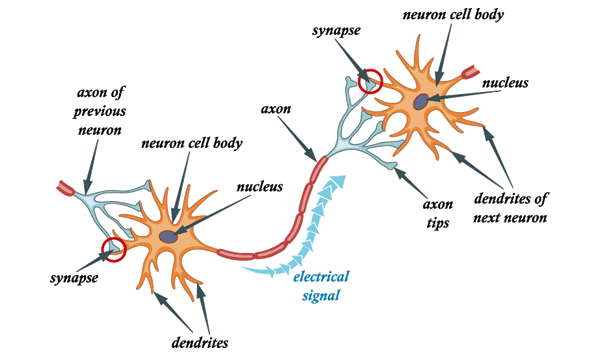
একটি সাধারণ নিউরনে কোষের দেহ, ডেনড্রাইটস এবং অ্যাক্সন থাকে। ডেনড্রাইটগুলি হ'ল পাতলা কাঠামো যা কোষের দেহ থেকে উত্থিত হয়। অ্যাক্সন একটি সেলুলার এক্সটেনশন যা এই কোষের শরীর থেকে উদ্ভূত হয়। বেশিরভাগ নিউরন ডেনড্রাইটের মাধ্যমে সংকেত গ্রহণ করে এবং অক্ষ বরাবর সংকেত প্রেরণ করে।

বেশিরভাগ সিনাপাসে সংকেতগুলি একটি নিউরনের অ্যাক্সন থেকে অন্যের ডেনড্রাইটে অতিক্রম করে। সমস্ত নিউরনগুলি তাদের ঝিল্লিতে ভোল্টেজ গ্রেডিয়েন্টগুলি রক্ষণাবেক্ষণের কারণে বৈদ্যুতিকভাবে উত্তেজক। যদি সংক্ষিপ্ত বিরতিতে ভোল্টেজটি পর্যাপ্ত পরিমাণে পরিবর্তিত হয়, তবে নিউরন একটি ক্রিয়াকলাপ বলে। একটি বৈদ্যুতিক রাসায়নিক পালস তৈরি করে। এই সম্ভাব্য অক্ষটি বরাবর দ্রুত ভ্রমণ এবং সিনেপটিক সংযোগগুলি তাদের কাছে পৌঁছানোর সাথে সাথে সক্রিয় করে।

এইভাবে, নিউরনগুলি পুরো নেটওয়ার্ক জুড়ে একে অপরের সাথে যোগাযোগ করতে পারে। একটি মানুষের মস্তিষ্কে শেখার প্রক্রিয়া এখনও পুরোপুরি বোঝা যায় নি, তবে বিজ্ঞানীরা পুরোপুরি নিশ্চিত যে নিউরনের মধ্যে সংযোগের শক্তি পরিবর্তন করে শেখার প্রক্রিয়াটি ব্যাখ্যা করা যেতে পারে।

নিউরনগুলি যে ক্রিয়াকলাপের সম্ভাবনাটিকে আরও বেশি পরিমাণে বিনিময় করে তাদের একে অপরের মধ্যে শক্তিশালী অ্যাক্সন সংযোগ থাকে এবং এর বিপরীতে। মানুষ হিসাবে আমরা যে কাজগুলি শিখি এবং নতুন অভিজ্ঞতা আমরা অর্জন করি, নিউরনের মধ্যে সংযোগের এই পরিবর্তনকে বাধ্য করে। কিছু নিউরন আরও আন্তঃসংযুক্ত হয়ে যায়, কিছু কম। কিছু সংযোগ এমনকি পুরোপুরি বন্ধ হয়ে যেতে পারে। আমাদের একটি নির্দিষ্ট কাজ সমাধান করার জন্য মানুষের জন্য, আমাদের মস্তিষ্কের জৈবিক নিউরাল নেটওয়ার্ককে এমন কিছু নিউরোনাল সংযোগ বিকাশ করতে হবে যাতে কিছু নিউরোন আরও আন্তঃসংযুক্ত থাকে এবং অন্যরা কম সংযুক্ত থাকে।

3. Artificial Neural Networks

জৈবিক নিউরাল নেটওয়ার্কগুলি কীভাবে কাজ করছে সে সম্পর্কে এখন আমাদের একটি প্রাথমিক ধারণা রয়েছে, আসুন কৃত্রিম নিউরাল নেটওয়ার্কের আর্কিটেকচারটি একবার দেখে নেওয়া যাক।

একটি নিউরাল নেটওয়ার্ক সাধারণত সংযুক্ত ইউনিট বা নোডের সংগ্রহ নিয়ে গঠিত। আমরা এই নোডগুলিকে নিউরন বলি। এই কৃত্রিম নিউরন আলগাভাবে আমাদের মস্তিষ্কের জৈবিক নিউরনের মডেল করে।

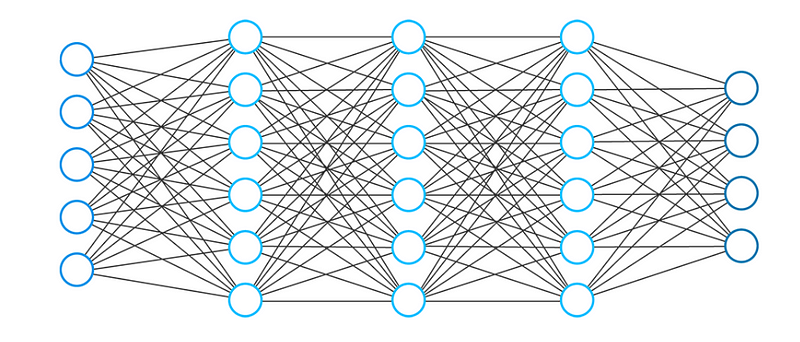
নিউরন হ'ল একটি সংখ্যাসূচক মানের উদীয়মান উপস্থাপনা (উদাঃ 1.2, 5.0, 42.0, 0.25, ইত্যাদি)। দুটি কৃত্রিম নিউরনের মধ্যে যে কোনও সংযোগকে বাস্তব জৈবিক মস্তিষ্কে অ্যাক্সন হিসাবে বিবেচনা করা যেতে পারে।

নিউরনের মধ্যে সংযোগগুলি তথাকথিত ওজন দ্বারা উপলব্ধি করা হয়, যা সংখ্যাগত মান ব্যতীত আর কিছুই নয়

নিউরনের মধ্যে ওজন নিউরাল নেটওয়ার্কের শেখার ক্ষমতা নির্ধারণ করে। জৈবিক স্নায়ুবহুল নেটওয়ার্কগুলির আগে যেমন উল্লেখ করা হয়েছে, শিখাকে নিউরনের মধ্যে সংযোগের শক্তির পরিবর্তনের মাধ্যমে ব্যাখ্যা করা যেতে পারে। একই নীতিটি কৃত্রিম নিউরাল নেটওয়ার্কের ক্ষেত্রে প্রযোজ্য।

যখন কোনও কৃত্রিম নিউরাল নেটওয়ার্ক শিখেন, নিউরনের মধ্যে ওজন পরিবর্তিত হয় এবং সংযোগের শক্তিও ঘটে অর্থ: প্রশিক্ষণ ডেটা এবং নির্দিষ্ট কাজের জন্য যেমন সংখ্যার শ্রেণিবিন্যাস দেওয়া হয়, আমরা নির্দিষ্ট সেট ওজনগুলির সন্ধান করি যা নিউরাল নেটওয়ার্ক সম্পাদন করতে দেয় শ্রেণিবিন্যাস। ওজনের সেট প্রতিটি কাজ এবং প্রতিটি ডেটাসেটের জন্য আলাদা। আমরা এই ওজনগুলির মানগুলি আগেই অনুমান করতে পারি না, তবে নিউরাল নেটওয়ার্কগুলি সেগুলি শিখতে হবে। শেখার প্রক্রিয়াটিকে আমরা প্রশিক্ষণও বলে থাকি।

4. Typical Neural Network Architecture

টিপিকাল নিউরাল নেটওয়ার্ক আর্কিটেকচারে বেশ কয়েকটি স্তর থাকে। আমরা প্রথম স্তরটিকে ইনপুট স্তর হিসাবে ডাকি। ইনপুট স্তর ইনপুট X ডেটা গ্রহণ করে যা থেকে নিউরাল নেটওয়ার্ক শিখে। হস্তাক্ষর সংখ্যার শ্রেণিবিন্যাসের আমাদের আগের উদাহরণে, এই ইনপুট X গুলি এই সংখ্যাগুলির চিত্রগুলি উপস্থাপন করবে (x মূলত একটি সম্পূর্ণ ভেক্টর যেখানে প্রতিটি প্রবেশিকা পিক্সেল হয়)। ইনপুট লেয়ারটিতে ভেক্টর এক্স-এ প্রবেশাধিকারী হিসাবে একই সংখ্যক নিউরন রয়েছে। অর্থ: প্রতিটি ইনপুট নিউরন ভেক্টর x এর একটি উপাদানকে উপস্থাপন করে।

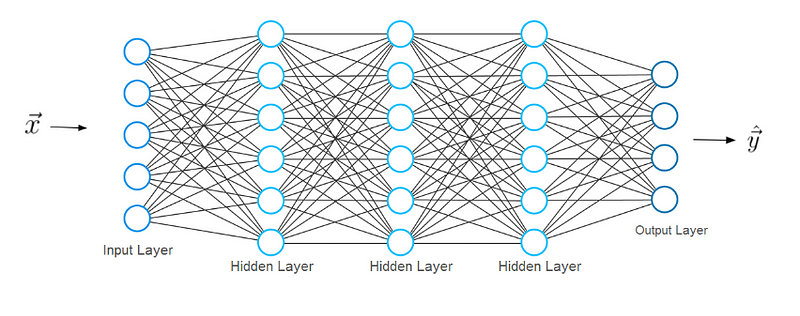
শেষ স্তরটিকে আউটপুট স্তর বলা হয়, যা স্নায়ুর নেটওয়ার্ক নিয়ে আসে এমন ফলাফলের প্রতিনিধিত্ব করে এমন একটি ভেক্টর ওয়াই আউটপুট দেয়। এই ভেক্টরের এন্ট্রিগুলি আউটপুট স্তরের নিউরনের মান উপস্থাপন করে। আমাদের শ্রেণিবিন্যাসের ক্ষেত্রে, শেষ স্তরের প্রতিটি নিউরন একটি আলাদা শ্রেণির প্রতিনিধিত্ব করবে। এই ক্ষেত্রে, আউটপুট নিউরনের একটি মান সম্ভাব্যতা দেয় যে এক্স বৈশিষ্ট্য দ্বারা প্রদত্ত হস্তাক্ষর অঙ্কটি সম্ভাব্য শ্রেণীর একটি (0-9 অঙ্কের একটি) এর সাথে সম্পর্কিত। আপনি যেমন কল্পনা করতে পারেন ক্লাস আছে আউটপুট নিউরন সংখ্যা একই হতে হবে।

পূর্বাভাস ভেক্টর y পাওয়ার জন্য, নেটওয়ার্ককে অবশ্যই কিছু গাণিতিক ক্রিয়াকলাপ করতে হবে। এই ক্রিয়াকলাপগুলি ইনপুট এবং আউটপুট স্তরগুলির মধ্যে স্তরগুলিতে সঞ্চালিত হয়। আমরা এই স্তরগুলিকে গোপন (ডীপ)স্তর বলি। আমরা এই স্তরগুলিকে গোপন স্তর বলি। এখন আমাদের আলোচনা করা যাক, স্তরগুলির মধ্যে সংযোগগুলি দেখতে কেমন লাগে।

5. Layer Connections in a Neural Network

শুধুমাত্র দুটি স্তর নিয়ে গঠিত নিউরাল নেটওয়ার্কের একটি ছোট উদাহরণ,  দয়া করে বিবেচনা করুন। ইনপুট স্তরটিতে দুটি ইনপুট নিউরন থাকে, যখন আউটপুট স্তরটিতে তিনটি নিউরন থাকে।

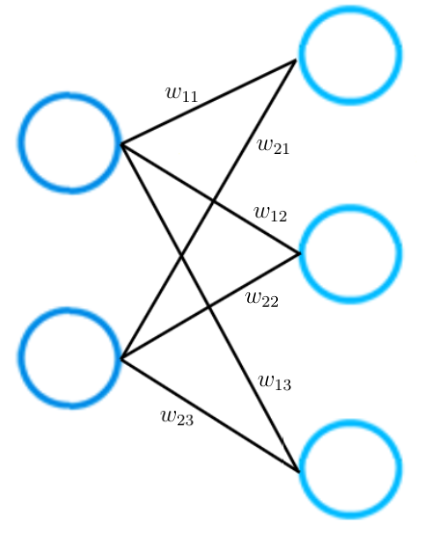
পূর্বে উল্লিখিত হিসাবে, দুটি নিউরনের মধ্যে প্রতিটি সংযোগ একটি সংখ্যাসূচক মান দ্বারা প্রতিনিধিত্ব করা হয়, যাকে আমরা ওজন বলি। ছবিতে আপনি দেখতে পাচ্ছেন, দুটি নিউরনের মধ্যে প্রতিটি সংযোগ আলাদা ওজন W  দ্বারা প্রতিনিধিত্ব করা হয়। এই ওজনের প্রত্যেকটির সূচক রয়েছে। সূচকের প্রথম মানটি স্তরের নিউরনের সংখ্যাকে বোঝায় যেখানে সংযোগটি উদ্ভূত হয়, সংযোগটি যে স্তরে নিউরনের সংখ্যার দিকে যায় তার মান দ্বিতীয় ।

এর অর্থ হ'ল প্রতিটি ইনডিস দুটি নিউরনকে আন্তঃসংযুক্ত করে উপস্থাপন করে। উদাহরণস্বরূপ, ওজন W 23 বুঝতে, প্রথম স্তরের দ্বিতীয় নিউরনের মধ্যে সংযোগ এবং দ্বিতীয় স্তরের তৃতীয় নিউরন।

দুটি নিউরাল নেটওয়ার্ক স্তরগুলির মধ্যে সমস্ত ওজনকে ম্যাট্রিক্স দ্বারা বোঝানো যেতে পারে যা ওয়েট ম্যাট্রিক্স বলে।

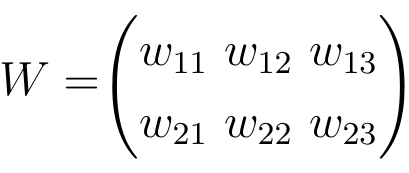
আপনি যেমন জানেন যে, কোনও ম্যাট্রিক্সের প্রতিটি এন্ট্রিতে একটি নির্দিষ্ট সারি এবং কলামে সেই প্রবেশের অবস্থানের ভিত্তিতে সূচক থাকে। ওজন ম্যাট্রিক্সের এন্ট্রিগুলি সংশ্লিষ্ট সূচকগুলির সাথে ওজনের মানগুলি উপস্থাপন করে।

নিউটনের মধ্যে সংযোগ রয়েছে বলে, একটি ওজন ম্যাট্রিক্সে একই সংখ্যক এন্ট্রি রয়েছে। এই ওজন ম্যাট্রিক্স দ্বারা সংযুক্ত দুটি স্তরগুলির আকার থেকে একটি ওজন ম্যাট্রিক্সের মাত্রাগুলি ফলাফল। সংযোগগুলি সূচিত হয় সে স্তরে নিউরনের সংখ্যার সাথে সারিগুলির সংখ্যার সাথে মিল রয়েছে এবং সংযোগগুলি যে স্তরের দিকে নিউরনের সংযোগ করে সেটির সাথে কলামের সংখ্যা মিলছে।

এই বিশেষ উদাহরণে, ওজন ম্যাট্রিক্সের সারিগুলির সংখ্যা ইনপুট স্তরের আকারের সাথে মিলিত হয় যা দুটি এবং আউটপুট স্তরের আকারের সাথে কলামগুলির সংখ্যা তিনটি।

6. একটি নিউরাল নেটওয়ার্ক শেখার প্রক্রিয়া

এখন যেহেতু আমরা নিউরাল নেটওয়ার্ক আর্কিটেকচারটি আরও ভালভাবে বুঝতে পারি, আমরা শিজ্ঞার প্রক্রিয়াটি স্বজ্ঞাতভাবে অধ্যয়ন করতে পারি। আমাদের ধাপে ধাপে এটি করা যাক। প্রথম পদক্ষেপটি ইতিমধ্যে আপনার জানা। প্রদত্ত ইনপুট বৈশিষ্ট্য ভেক্টর এক্স এর জন্য, নিউরাল নেটওয়ার্ক একটি পূর্বাভাস ভেক্টর গণনা করে, যা আমরা এখানে h হিসাবে ডাকি।

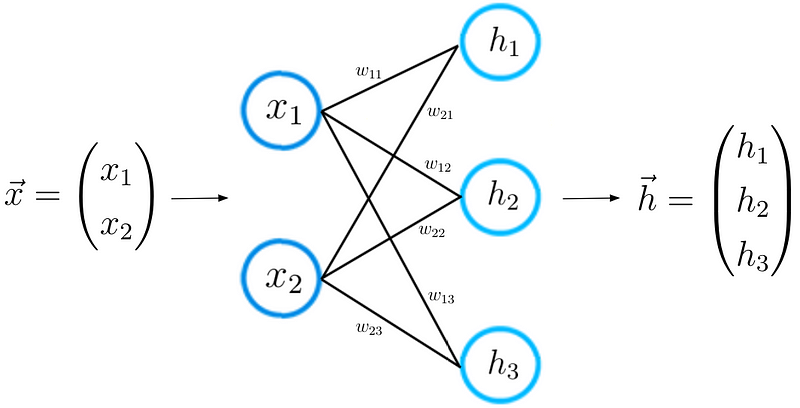
এই পদক্ষেপটি এগিয়ে প্রচার হিসাবেও চিহ্নিত করা হয়। ইনপুট ভেক্টর X এবং ওজন ম্যাট্রিক্স W দুটি নিউরন স্তর সংযুক্ত করে, আমরা ভেক্টর X এবং ম্যাট্রিক্স W এর মধ্যে ডট পণ্যটি গণনা করি

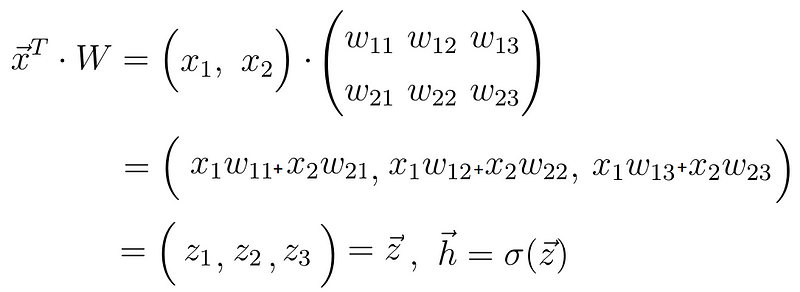
এই ডট পণ্যটির ফলাফলটি আবার ভেক্টর, যা আমরা z বলি। চূড়ান্ত পূর্বাভাস ভেক্টর এইচ ভেক্টর z তে তথাকথিত অ্যাক্টিভেশন ফাংশন প্রয়োগ করে প্রাপ্ত হয়। এই ক্ষেত্রে, অ্যাক্টিভেশন ফাংশন সিগমা অক্ষর দ্বারা প্রতিনিধিত্ব করা হয়। একটি অ্যাক্টিভেশন ফাংশনটি কেবল একটি ননলাইনার ফাংশন যা z থেকে h এ ননলাইনার ম্যাপিং সম্পাদন করে। ডিপ লার্নিংয়ে 3 টি অ্যাক্টিভেশন ফাংশন ব্যবহৃত হয়,

which are tanh, sigmoid and ReLu.

এই মুহুর্তে, আপনি স্নায়বিক নেটওয়ার্কে নিউরনের পিছনে অর্থটি চিনতে পারেন। একটি নিউরন হ'ল সংখ্যাসমূহের উপস্থাপনা।

ইনপুট স্তরগুলির নিউরনগুলি ইনপুট বৈশিষ্ট্যগুলির x এর মান উপস্থাপন করে। আউটপুট স্তরের নিউরনগুলি নিউরাল নেটওয়ার্ক গণনা করা পূর্বাভাসকে উপস্থাপন করে। লুকানো স্তরের নিউরনের মানগুলি মূলত কয়েকটি মধ্যবর্তী মান যা গণনার জন্য ব্যবহৃত হয়।

আসুন এক মুহুর্তের জন্য ভেক্টর জেডকে ঘনিষ্ঠভাবে দেখি। আপনি দেখতে পাচ্ছেন, z এর প্রতিটি উপাদান ইনপুট ভেক্টর x দিয়ে থাকে। এই মুহুর্তে, ওজনের ভূমিকাটি সুন্দরভাবে ফুটে উঠেছে। একটি স্তরের নিউরনের একটি মান কিছু সংখ্যাসূচক মান দ্বারা ভারিত পূর্ববর্তী স্তরের নিউরনের মানগুলির একটি লিনিয়ার সংমিশ্রণ নিয়ে গঠিত। এই সংখ্যাসূচক মানগুলি এমন ওজন যা আমাদের জানায় যে এই নিউরনগুলি একে অপরের সাথে কতটা দৃ .়ভাবে সংযুক্ত রয়েছে।

প্রশিক্ষণের সময়, এই ওজনগুলি সমন্বয় করা হয়, কিছু নিউরন আরও সংযুক্ত হয়ে যায়, কিছু নিউরন কম সংযুক্ত হয়ে ওঠে। জৈবিক নিউরাল নেটওয়ার্কের মতো, শেখার অর্থ ওজনের পরিবর্তন। তদনুসারে, z, h এবং চূড়ান্ত আউটপুট ভেক্টর y এর মান ওজনগুলির সাথে পরিবর্তিত হচ্ছে। কিছু ওজন আমাদের নিউরাল নেটওয়ার্কের ভবিষ্যদ্বাণীগুলি প্রকৃত স্থল সত্য ভেক্টর y_hat এর কাছাকাছি করে তোলে, কিছু ওজন স্থল সত্য ভেক্টরের দূরত্ব বাড়িয়ে তোলে।

এখন আমরা যখন জানি যে দুটি নিউরাল নেটওয়ার্ক স্তরগুলির মধ্যে গাণিতিক গণনাগুলি কেমন দেখায়, আমরা আমাদের জ্ঞানটি একটি 5 টি স্তরযুক্ত গভীরতর স্থাপত্যে প্রসারিত করতে পারি।

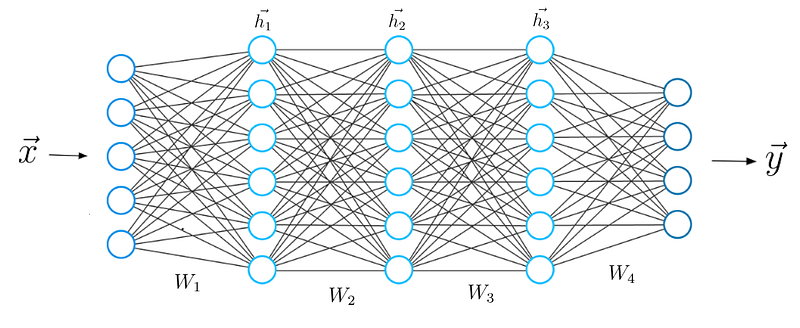
পূর্বের মতো একইভাবে আমরা ইনপুট X এবং প্রথম ওজন ম্যাট্রিক্স W 1 এর মধ্যে ডট পণ্য গণনা করি এবং প্রথম লুকানো ভেক্টর h 1 পেতে ফলাফল ভেক্টরে একটি অ্যাক্টিভেশন ফাংশন প্রয়োগ করি। h1 এখন আসন্ন তৃতীয় স্তর জন্য ইনপুট হিসাবে বিবেচনা করা হয়। চূড়ান্ত আউটপুট y না পাওয়া পর্যন্ত পূর্ব থেকে সম্পূর্ণ প্রক্রিয়াটি পুনরাবৃত্তি করা হয়:

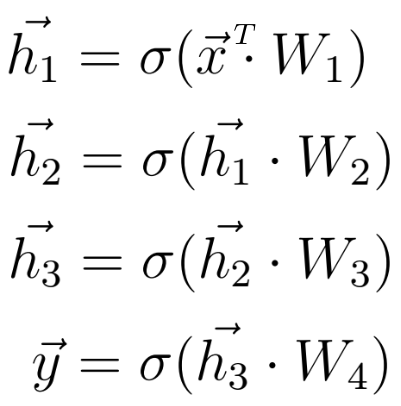
7. ক্ষতি ফাংশন

আমরা নিউরাল নেটওয়ার্কের পূর্বাভাস পাওয়ার পরে, দ্বিতীয় ধাপে আমাদের অবশ্যই এই পূর্বাভাস ভেক্টরকে আসল ভিত্তির সত্য লেবেলের সাথে তুলনা করতে হবে। আমরা গ্রাউন্ড ট্রুথ লেবেলটিকে ভেক্টর হিসাবে y_hat বলি। ভেক্টর ওয়াইয়ের পূর্বাভাস চলাকালীন নিউরাল নেটওয়ার্ক গণনা করা হয়েছে এমন পূর্বাভাস রয়েছে (এবং যা বাস্তবে প্রকৃত মান থেকে খুব আলাদা হতে পারে), ভেক্টর ওয়াই_তে প্রকৃত মান রয়েছে।

গাণিতিকভাবে, আমরা ক্ষতির ক্রিয়াটি নির্ধারণ করে y এবং y_hat এর মধ্যে পার্থক্যটি পরিমাপ করতে পারি যা মান এই পার্থক্যের উপর নির্ভর করে।

সাধারণ লোকসানের কার্যকারণের উদাহরণ হ'ল চতুর্ভুজ হ্রাস:

যেহেতু পূর্বাভাস ভেক্টর y নিউরাল নেটওয়ার্কের ওজনগুলির একটি ফাংশন (যা আমরা থেইটা সংক্ষেপে সংক্ষেপে দেখি), ক্ষতিটি ওজনগুলিরও একটি কার্য।

এই ক্ষতির ফাংশনের মান y_hat এবং y এর মধ্যে পার্থক্যের উপর নির্ভর করে। একটি উচ্চতর পার্থক্য মানে একটি উচ্চ ক্ষতির মান, একটি ছোট পার্থক্যের অর্থ একটি ক্ষতির ক্ষতির মান। ভবিষ্যদ্বাণী এবং লেবেলের মধ্যে পার্থক্য হ্রাস হওয়ায় ক্ষতির ফাংশনটি হ্রাস করা সরাসরি নিউরাল নেটওয়ার্কের আরও সঠিক ভবিষ্যদ্বাণীগুলির দিকে নিয়ে যায়।

আসলে, ক্ষতির ফাংশনটি হ্রাস করা হ'ল একমাত্র উদ্দেশ্য যা নিউরাল নেটওয়ার্কটি অর্জন করার চেষ্টা করে। মনে রাখবেন যখন আমি বলেছিলাম যে নিউরাল নেটওয়ার্ক স্পষ্টভাবে কোনও কার্য-নির্দিষ্ট বিধি দ্বারা প্রোগ্রাম না করেই কাজগুলি সমাধান করে। এটি সম্ভব কারণ লক্ষ্য হিসাবে ক্ষতির ফাংশনটি হ্রাস করা সর্বজনীন এবং এটি কার্য বা কার্য পরিস্থিতিতে নির্ভর করে না।

ক্ষতির ফাংশনটি হ্রাস করার কারণে স্বয়ংক্রিয়ভাবে নিউরাল নেটওয়ার্ক মডেলটি হাতের কাজটির সঠিক বৈশিষ্ট্য নির্বিশেষে আরও ভাল পূর্বাভাস দেয় causes আপনাকে কেবল কাজের জন্য সঠিক ক্ষতি ফাংশনটি নির্বাচন করতে হবে। সৌভাগ্যক্রমে, কেবলমাত্র দুটি ক্ষতি ফাংশন রয়েছে যা আপনার অনুশীলনের মধ্যে সম্মুখীন হওয়া প্রায় কোনও সমস্যা সমাধানের জন্য জানা উচিত।

এই ক্ষতির কাজগুলি হ'ল ক্রস-এন্ট্রপি ক্ষতি:

and the Mean Squared Error Loss:

যেহেতু ক্ষতি ওজনের উপর নির্ভর করে, তাই আমাদের অবশ্যই ওজনের একটি নির্দিষ্ট সেট খুঁজে বের করতে হবে যার জন্য ক্ষতির ফাংশনের মান যতটা সম্ভব কম। ক্ষতির ফাংশন হ্রাস করার পদ্ধতিটি গ্রেডিয়েন্ট ডেসেন্ট নামে একটি পদ্ধতি দ্বারা গাণিতিকভাবে অর্জন করা হয়।

এই নিউরাল নেটওয়ার্কটি একটি ইনপুট এক্স পায় এবং পূর্বাভাস y করে। যাক এই নিউরাল নেটওয়ার্কের প্রাথমিক ওজনের মান 5 এবং ইনপুট x 2 হয় Therefore সুতরাং এই নেটওয়ার্কটির ভবিষ্যদ্বাণী y এর মান 10 হয়, তবে y_hat লেবেলের মান 6 হতে পারে।

এর অর্থ হল যে পূর্বাভাসটি সঠিক নয় এবং আমাদের অবশ্যই একটি নতুন ওজন মান সন্ধানের জন্য গ্রেডিয়েন্ট বংশদ্ভুত পদ্ধতিটি ব্যবহার করতে হবে যা নিউরাল নেটওয়ার্ককে সঠিক পূর্বাভাস দেয়। প্রথম পদক্ষেপে, আমাদের অবশ্যই কাজের জন্য একটি ক্ষতি ফাংশন বেছে নিতে হবে। এর আগে আমি যে দ্বিঘাতের ক্ষতিটি সংজ্ঞায়িত করেছি তা গ্রহণ করি এবং এই ফাংশনটির পরিকল্পনা করি যা মূলত একটি চতুর্ভুজ ফাংশন:

y -অক্ষটি হ্রাস মান যা লেবেল এবং পূর্বাভাসের মধ্যে পার্থক্য এবং এইভাবে নেটওয়ার্ক পরামিতি উপর নির্ভর করে, এক্ষেত্রে এক ওজন w। x -অক্ষ এই ওজনের জন্য মানগুলি উপস্থাপন করে। আপনি দেখতে পাচ্ছেন যে একটি নির্দিষ্ট ওজন W রয়েছে যার জন্য লোকসানের কার্যকারিতা বিশ্বব্যাপী সর্বনিম্ন পৌঁছে যায়। এই মানটি হ'ল অনুকূল ওজন পরামিতি যা নিউরাল নেটওয়ার্ককে সঠিক ভবিষ্যদ্বাণী তৈরি করতে পারে যা 6.. এই ক্ষেত্রে, সর্বোত্তম ওজনের জন্য মানটি হবে 3:

অন্যদিকে, আমাদের প্রাথমিক ওজন 5, যা মোটামুটি উচ্চ ক্ষতির দিকে নিয়ে যায়। এখন লক্ষ্যটি হ'ল বারবার ওজনের প্যারামিটার আপডেট করা যতক্ষণ না আমরা সেই নির্দিষ্ট ওজনের সর্বোত্তম মান পৌঁছায় না। এই সময়টি যখন আমাদের ক্ষতির ফাংশনের গ্রেডিয়েন্ট ব্যবহার করা প্রয়োজন। ভাগ্যক্রমে, এক্ষেত্রে, ক্ষতির ফাংশনটি একটি একক ভেরিয়েবলের ফাংশন, যা ওজন ডব্লিউ:

In the next step, we calculate the derivative of the loss function with respect to this parameter:

চূড়ান্ত পদক্ষেপে, আমরা আমাদের যুদ্ধের উন্নতি করার প্রচেষ্টা হিসাবে একটি গ্রেডিয়েন্ট বংশোদ্ভূত পদক্ষেপ সম্পাদন করি। আমরা আপনার বর্তমান ওজনকে ওজনকে যে ওজনের জন্য নেতিবাচক গ্রেডিয়েন্ট অনুসারে ক্ষতির ক্রিয়াটির মূল্য হ্রাস করে তার দিকে আপডেট করতে আমরা এই নেতিবাচক গ্রেডিয়েন্টটি ব্যবহার করি:

এই সমীকরণের ফ্যাক্টর এপসিলন হ'ল লার্নিং রেট নামে পরিচিত একটি হাইপারপ্যারামিটার। শেখার হার নির্ধারণ করে যে আপনি প্যারামিটারগুলি কত দ্রুত বা কত ধীরে ধীরে আপডেট করতে চান। দয়া করে মনে রাখবেন যে শিখার হারটি সেই উপাদানটি যা আমাদের সাথে নেতিবাচক গ্রেডিয়েন্টকে গুণ করতে হয় এবং শেখার হারটি সাধারণত খুব কম থাকে। আমাদের ক্ষেত্রে, শিক্ষার হার 0.1।

যেমন আপনি দেখতে পাচ্ছেন, গ্রেডিয়েন্ট বংশোদ্ভূত হওয়ার পরে আমাদের ওজন এখন গ্রেডিয়েন্ট স্টেপের আগে 4.2 এবং সর্বোত্তম ওজনের চেয়ে কাছে।

নতুন ওজন মানের জন্য ক্ষতির ফাংশনের মানটিও কম, যার অর্থ নিউরাল নেটওয়ার্ক এখন আরও ভাল ভবিষ্যদ্বাণী করতে সক্ষম। আপনি আপনার মাথায় গণনা করতে পারেন এবং দেখুন যে নতুন ভবিষ্যদ্বাণীটি আসলে আগের চেয়ে লেবেলের কাছাকাছি।

প্রতিবার যখন আমরা ওজনের হালনাগাদ সম্পাদনা করি তখন আমরা নেতিবাচক গ্রেডিয়েন্টটিকে নীচের ওজনের দিকে এগিয়ে যাই।

প্রতিটি গ্রেডিয়েন্ট বংশদ্ভুত পদক্ষেপ বা ওজন আপডেটের পরে, নেটওয়ার্কের বর্তমান ওজন সর্বোত্তম ওজনের কাছাকাছি পৌঁছে যায় যতক্ষণ না অবশেষে আমরা তাদের কাছে পৌঁছে যাই এবং নিউরাল নেটওয়ার্কটি আমাদের যে ভবিষ্যদ্বাণী করতে চাইবে তা করতে সক্ষম হবে।