source 
please refer to this article

এই নিবন্ধে, আমি আপনাকে ডিপ লার্নিংয়ের সবচেয়ে পরিশীলিত অপ্টিমাইজেশন অ্যালগরিদমগুলি উপস্থাপন করব যা নিউরাল নেটওয়ার্কগুলি দ্রুত শিখতে এবং আরও ভাল পারফরম্যান্স অর্জন করতে দেয়। এই অ্যালগরিদমগুলি হ'ল: মোমেন্টাম, অ্যাডাগ্রাড, আরএমএসপ্রপ এবং অ্যাডাম অপটিমাইজার সহ স্টোকাস্টিক গ্রেডিয়েন্ট বংশোদ্ভূত। 

1. Why do we need better optimization Algorithms?

আমি মনে করি আপনার এখন অবধি জানা উচিত, এর পিছনে গাণিতিক পদ্ধতিটিকে গ্রেডিয়েন্ট বংশোদ্ভূত বলা হয়। আপনি যদি এই বিষয়টির সাথে পরিচিত না হন তবে দয়া করে এই নিবন্ধটি দেখুন, যেখানে আমরা আরও বিস্তারিতভাবে গ্রেডিয়েন্ট বংশোদ্ভূত আবরণ।

এই কৌশলটিতে, আমাদের যে ওজনগুলি উন্নত করতে চাই তার ক্ষেত্রে আমাদের ক্ষতির ফাংশনের গ্রেডিয়েন্ট গণনা করতে হবে। পরবর্তীকালে, ওজনগুলি গ্রেডিয়েন্টের নেতিবাচক দিকের দিকে আপডেট হয়। পর্যায়ক্রমে ওজনগুলিতে গ্রেডিয়েন্ট বংশদ্ভুত প্রয়োগ করার পরে, আমরা শেষ পর্যন্ত অনুকূল ওজনে পৌঁছাব যা ক্ষতির ক্রিয়াকে হ্রাস করে এবং নিউরাল নেটওয়ার্ককে আরও ভাল ভবিষ্যদ্বাণী করতে দেয়। এখনও পর্যন্ত তত্ত্ব।

আমাকে ভুল করবেন না, গ্রেডিয়েন্ট বংশোদ্ভূত এখনও একটি শক্তিশালী কৌশল। বাস্তবে, তবে এই কৌশলটি প্রশিক্ষণের সময় কিছু সমস্যার মুখোমুখি হতে পারে যা শিখার প্রক্রিয়াটি ধীর করে দিতে পারে বা সবচেয়ে খারাপ ক্ষেত্রে এমনকি অ্যালগরিদমকে সর্বোত্তম ওজন খুঁজে পাওয়া থেকে বাধা দেয় prevent

এই সমস্যাগুলি একদিকে ক্ষতির পয়েন্ট এবং ক্ষতির ফাংশনের স্থানীয় মিনিমা ছিল, যেখানে ক্ষতির ফাংশন সমতল হয় এবং গ্রেডিয়েন্টটি শূন্যে যায়:

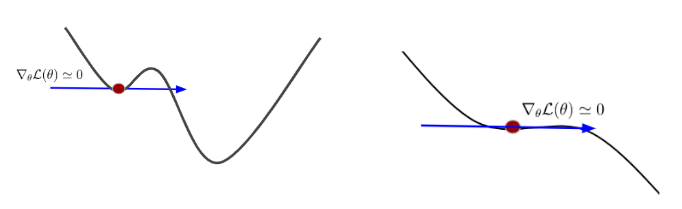
শূন্যের কাছাকাছি একটি গ্রেডিয়েন্ট ওজনের পরামিতিগুলিতে উন্নতি করে না এবং পুরো শেখার প্রক্রিয়াটিকে বাধা দেয়।

অন্যদিকে, আমাদের গ্রেডিয়েন্টগুলি শূন্যের কাছাকাছি না থাকলেও, প্রশিক্ষণ সেট থেকে বিভিন্ন ডেটা নমুনার জন্য গণনা করা এই গ্রেডিয়েন্টগুলির মান এবং দিকনির্দেশে ভিন্ন হতে পারে। আমরা বলি যে গ্রেডিয়েন্টগুলি কোলাহলপূর্ণ বা প্রচুর বৈকল্পিক রয়েছে। এটি সর্বোত্তম ওজনের দিকে জিগজ্যাগের চলাচলের দিকে পরিচালিত করে এবং শেখা আরও ধীর করে তুলতে পারে:

নিম্নলিখিত নিবন্ধে, আমরা আরও পরিশীলিত গ্রেডিয়েন্ট বংশদ্ভুত অ্যালগরিদম সম্পর্কে শিখতে চলেছি। এই সমস্ত অ্যালগোরিদমগুলি নিয়মিত গ্রেডিয়েন্ট বংশোদ্ভূত অপ্টিমাইজেশানের উপর ভিত্তি করে তৈরি করা হয়েছে যা আমরা এ পর্যন্ত জানি। তবে আমরা আরও কিছু কার্যকর অপ্টিমাইজেশন অ্যালগরিদম তৈরি করতে কিছু গাণিতিক কৌশল দ্বারা ওজন অপ্টিমাইজেশনের জন্য এই নিয়মিত পদ্ধতির প্রসারিত করতে পারি যা আমাদের নিউরাল নেটওয়ার্কগুলিকে পর্যাপ্ত পরিমাণে এই সমস্যাগুলি পরিচালনা করতে দেয়, তত দ্রুত শিখতে এবং আরও ভাল পারফরম্যান্স অর্জন করতে

আমি আপনাকে যে পরিশীলিত অ্যালগরিদমগুলি উপস্থাপন করতে চাই তার মধ্যে প্রথমটিকে স্টোকাস্টিক গ্রেডিয়েন্ট বংশোদ্ভূত বিকাশ বলে।

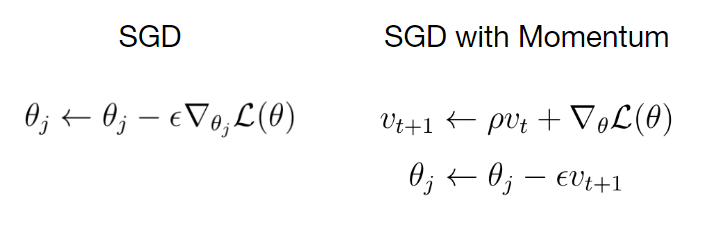
বাম দিকে, আপনি নিয়মিত স্টোকাস্টিক স্টোকাস্টিক গ্রেডিয়েন্ট বংশোদ্ভূত অনুযায়ী ওজন আপডেটের সমীকরণটি দেখতে পারেন। ডানদিকে সমীকরণটি গতির সাথে SGD অনুযায়ী ওজন আপডেটের নিয়মটি দেখায়। গতিবেগ অতিরিক্ত হিসাবে উপস্থিত হয় পদ ρ বার v । এটি নিয়মিত আপডেট নিয়মে যুক্ত করা হয়।

স্বজ্ঞাতভাবে বলতে গেলে, এই গতির পদটি যুক্ত করে আমরা আমাদের গ্রেডিয়েন্টকে প্রশিক্ষণের সময় এক ধরণের বেগ v তৈরি করতে দিই। বেগ হ'ল গ্রেডিয়েন্ট দ্বারা ওজনযুক্ত গ্রেডিয়েন্টের চলমান যোগফল ρ

ρ ঘর্ষণ হিসাবে বিবেচনা করা যেতে পারে, যা বেগ কিছুটা কমিয়ে দেয়।

সাধারণভাবে, আপনি দেখতে পাবে যে গতিবেগটি সময়ের সাথে সাথে গড়ে ওঠে। গতিময় শব্দটি স্যাডল পয়েন্ট এবং স্থানীয় মিনিমা ব্যবহার করে। গ্রেডিয়েন্টের জন্য কম বিপজ্জনক হয়ে উঠুন।

কারণ বৈশ্বিক ন্যূনতমের দিকে ধাপের মাপ এখন কেবলমাত্র বর্তমান সময়ে ক্ষতি ফাংশনের গ্রেডিয়েন্টের উপর নির্ভর করে না, সময়ের সাথে সাথে গতিবেগের উপরেও নির্ভর করে।

অন্য কথায়, আমরা একটি নির্দিষ্ট বিন্দুতে গ্রেডিয়েন্টের চেয়ে বেশি বেগের দিকের দিকে এগিয়ে চলেছি।

আপনি যদি গতিযুক্ত স্টোকাস্টিক গ্রেডিয়েন্ট বংশোদ্ভূত দৈহিক উপস্থাপনা পেতে চান তবে এমন একটি বলের কথা চিন্তা করুন যা একটি পাহাড়ের নিচে গড়িয়ে পড়ে এবং সময়ের সাথে সাথে গতি বাড়িয়ে তোলে। এই বলটি যদি কিছু পথে বাধা যেমন কোনও গর্ত বা সমতল স্থল যার নীচে  না পৌঁছায়, বেগ v এই বাধাগুলি পেরিয়ে বলটিকে যথেষ্ট শক্তি দেবে। এই ক্ষেত্রে, ফ্ল্যাট গ্রাউন্ড এবং গর্তটি ক্ষতির কার্যকারীর কাটি পয়েন্ট বা স্থানীয় মিনিমা উপস্থাপন করে।

এই ভিডিওতে, আমি আপনাকে গতিময় মেয়াদের সাথে নিয়মিত স্টোকাস্টিক গ্রেডিয়েন্ট বংশোদ্ভূত এবং স্টোকাস্টিক গ্রেডিয়েন্ট বংশোদ্ভুতের সরাসরি তুলনা দেখাতে চাই। উভয় অ্যালগরিদম 3 ডি স্পেসে বাস করে এমন ক্ষতির ক্রিয়াকলাপটি সর্বনিম্ন পৌঁছানোর চেষ্টা করছে। অনুগ্রহ করে নোট করুন কীভাবে গতিশীল শব্দটি গ্রেডিয়েন্টগুলিকে কম বৈকল্পিকতা এবং কম জিগ-জাগ আন্দোলন করে তোলে।

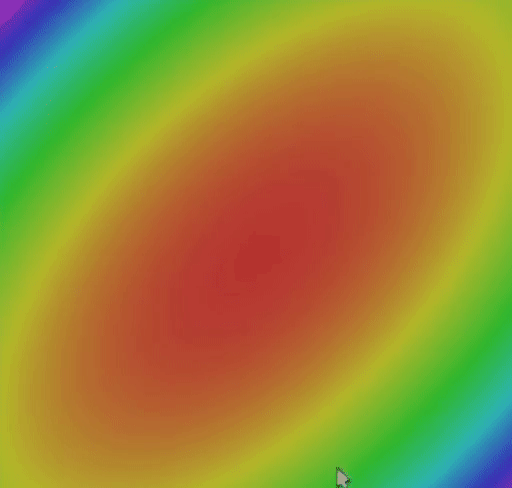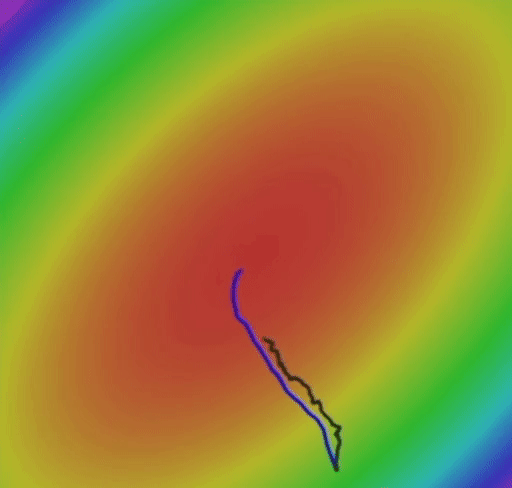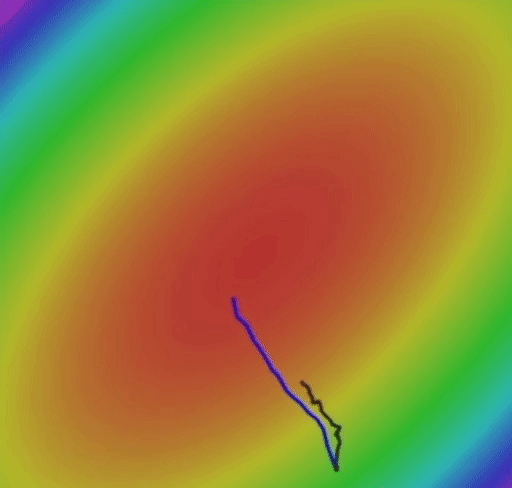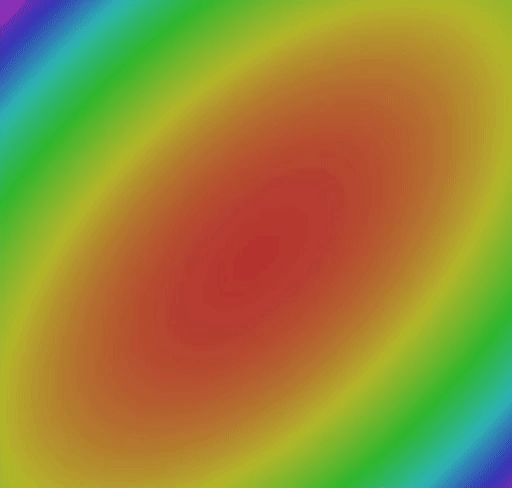
সাধারণভাবে, গতিময় শব্দটি সর্বোত্তম ওজনের দিকে আরও স্থিতিশীল এবং দ্রুত রূপান্তরিত করে।

আর একটি অপ্টিমাইজেশান কৌশলকে বলা হয় অ্যাডাগ্রেড। ধারণাটি হল আপনি অপ্টিমাইজেশনের সময় স্কোয়ার গ্রেডিয়েন্টের চলমান যোগফল রাখবেন। এই ক্ষেত্রে, আমাদের কোনও গতিময় পদ নেই, তবে একটি এক্সপ্রেশন G যা স্কোয়ার গ্রেডিয়েন্টগুলির যোগফল।

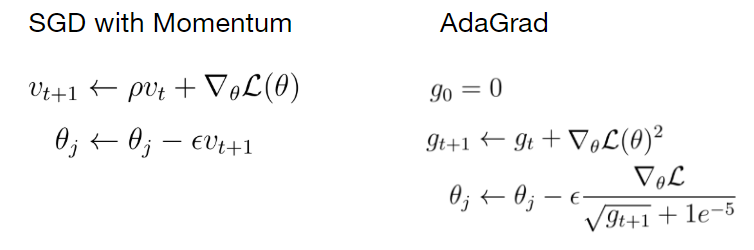
যখন আমরা একটি ওজন পরামিতি আপডেট করি, আমরা সেই শব্দটি জি এর মূল দ্বারা বর্তমান গ্রেডিয়েন্টকে বিভক্ত করি। অ্যাডগ্র্যাডের পিছনে অন্তর্দৃষ্টি বোঝাতে, একটি দ্বি-মাত্রিক স্থানে একটি ক্ষতির ফাংশনটি কল্পনা করুন যেখানে একটি দিকের ক্ষতির ক্রিয়াকলাপটি খুব ছোট এবং অন্যদিকে খুব উচ্চ। অক্ষগুলি বরাবর গ্রেডিয়েন্টগুলি সংক্ষেপ করে যেখানে গ্রেডিয়েন্টগুলি ছোট হয় এই গ্রেডিয়েন্টগুলির বর্গাকার যোগফল আরও ছোট হয়ে যায়। যদি আপডেটের পদক্ষেপের সময়, আমরা বর্তমান গ্রেডিয়েন্টকে একটি খুব সামান্য স্কোয়ার্ড গ্রেডিয়েন্ট g দ্বারা বিভক্ত করি, সেই বিভাগের ফলাফলটি খুব উচ্চতর হয় এবং উচ্চতর গ্রেডিয়েন্ট মান সহ অন্যান্য অক্ষের বিপরীতে।

এর অর্থ হ'ল আমরা অক্ষের সাথে ধীরে ধীরে গ্রেডিয়েন্টটি বাড়িয়ে অক্ষের সাথে আপডেট প্রসেসটি ত্বরান্বিত করি। অন্যদিকে, বড় গ্রেডিয়েন্ট সহ অক্ষ বরাবর আপডেটগুলি কিছুটা ধীরে ধীরে।

ফলস্বরূপ, আমরা অ্যালগরিদমকে একই অনুপাত সহ যে কোনও দিকে আপডেট করতে বাধ্য করি।

তবে এই অপ্টিমাইজেশন অ্যালগরিদম নিয়ে একটি সমস্যা আছে। প্রশিক্ষণ যখন দীর্ঘ সময় নেয় তখন স্কোয়ার গ্রেডিয়েন্টগুলির যোগফলের কী হবে তা কল্পনা করুন।

সময়ের সাথে সাথে, এই পদটি আরও বড় হবে। যদি বর্তমান গ্রেডিয়েন্টটি এই বৃহত সংখ্যায় ভাগ করা হয় তবে ওজনগুলির জন্য আপডেটের ধাপটি খুব ছোট হয়ে যায়। এটি এমনভাবে হয় যেন আমরা খুব কম শিক্ষার ব্যবহার করি যা প্রশিক্ষণটি আরও কম হয়ে যায়। সবচেয়ে খারাপ ক্ষেত্রে, আমরা অ্যাডগ্রাডের সাথে আটকে যাব এবং প্রশিক্ষণ চিরতরে চলতে থাকবে।

আরএমএসপ্রপ নামে আডাগ্রাডের সামান্য প্রকরণ রয়েছে যা অ্যাডাগ্রাডের সমস্যার সমাধান করে। আরএমএসপ্রপ দিয়ে আমরা স্কোয়ার গ্রেডিয়েন্টগুলির চলমান যোগফলটি এখনও রাখি কিন্তু প্রশিক্ষণের সময়কালে সেই পরিমাণটি ক্রমাগত বাড়তে দেয় না তার পরিবর্তে আমরা সেই পরিমাণটি ক্ষয় হতে দেয়।

আরএমএসপ্রপতে আমরা স্কোয়ার গ্রেডিয়েন্টের যোগফলকে ক্ষয় হার by দ্বারা গুণিত করি এবং বর্তমান গ্রেডিয়েন্টকে ওয়েট (1- α) দ্বারা যুক্ত করি। আরএমএসপ্রপের ক্ষেত্রে আপডেটের ধাপটি ঠিক অ্যাডগ্রাডের মতোই দেখাচ্ছে যেখানে আমরা বর্তমান গ্রেডিয়েন্টকে এক মাত্রার সাথে আন্দোলনকে ত্বরান্বিত করার এবং অন্যান্য মাত্রা সহ আন্দোলনকে গতি কমিয়ে দেওয়ার এই দুর্দান্ত সম্পত্তি অর্জনের জন্য বর্গক্ষেত্রের গ্রেডিয়েন্টের যোগফল দ্বারা বিভক্ত করি।

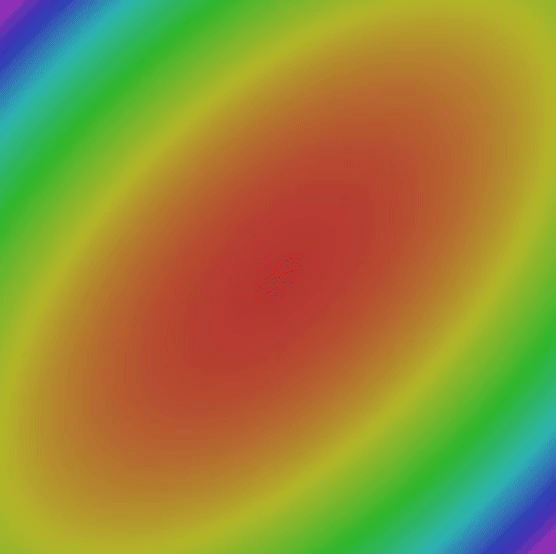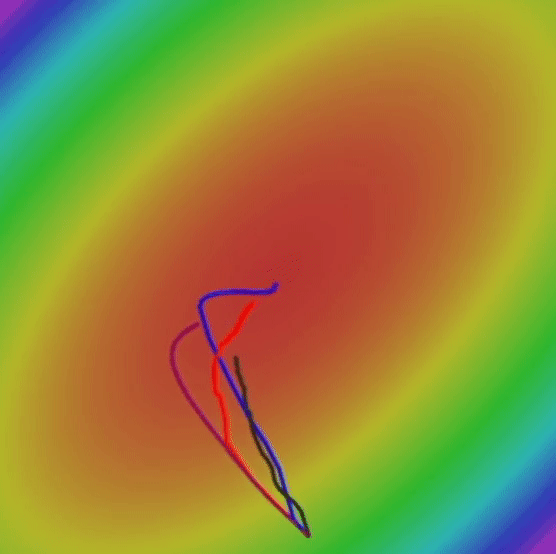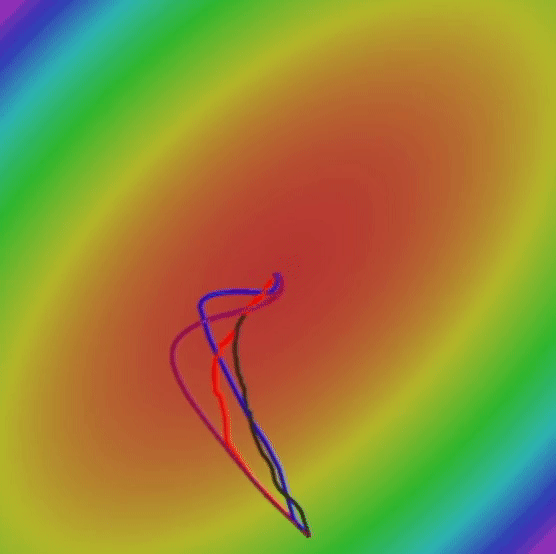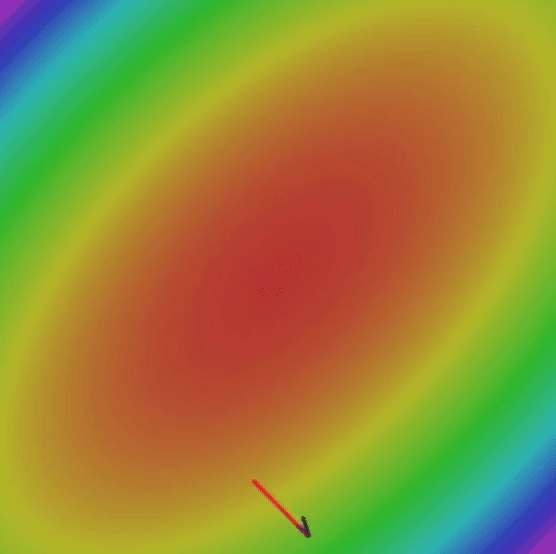
আসুন দেখি যে RMSProp কীভাবে এসজিডি এবং এসজিডি এর তুলনায় তুলনামূলকভাবে সর্বোত্তম ওজনগুলি সন্ধান করার জন্য করছে।

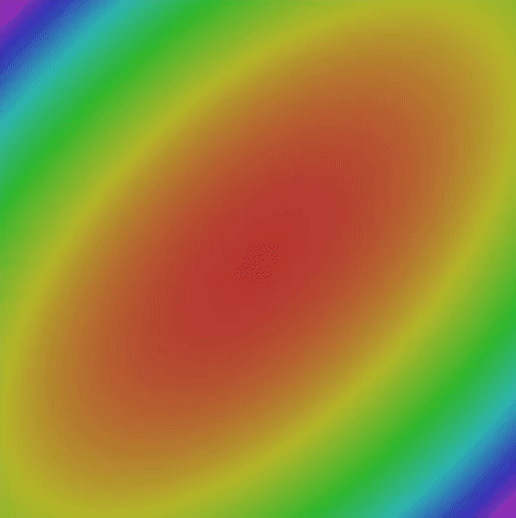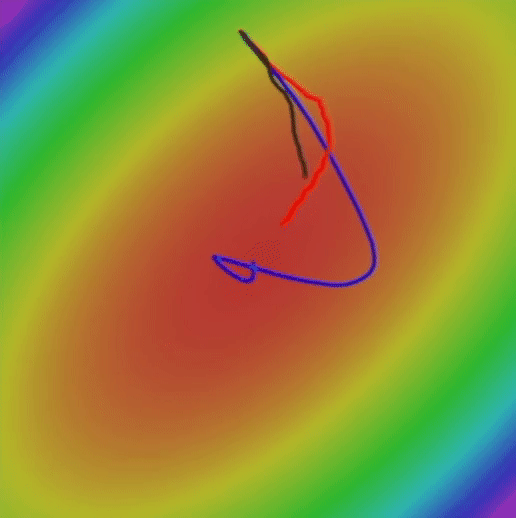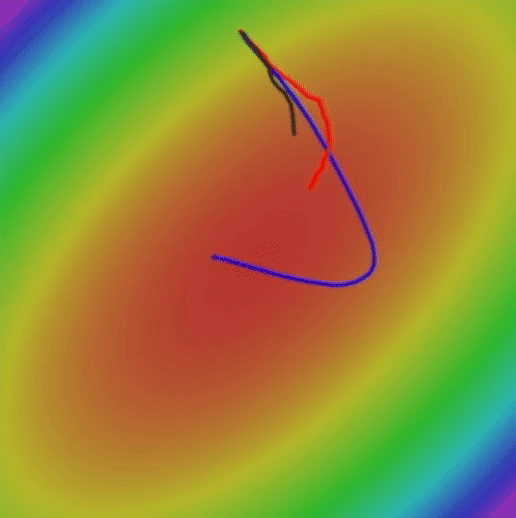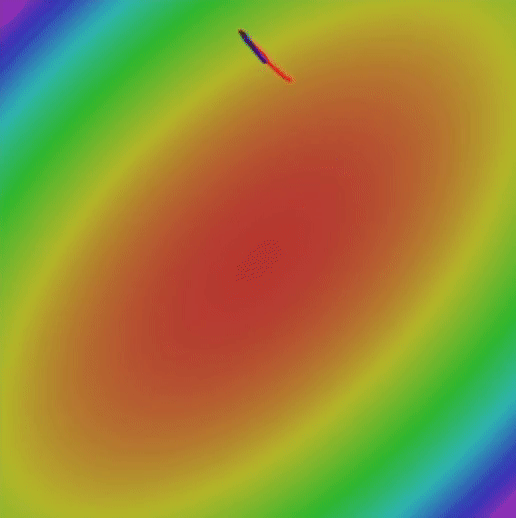
যদিও গতিযুক্ত এসজিডি গ্লোবাল ন্যূনতম দ্রুততম খুঁজে পেতে সক্ষম হয়েছে, এই অ্যালগরিদম অনেক দীর্ঘ পথ নেয়, এটি বিপজ্জনক হতে পারে। কারণ দীর্ঘতর পথটির অর্থ আরও সম্ভাব্য স্যাডল পয়েন্ট এবং স্থানীয় মিনিমা। অন্যদিকে, আরএমএসপ্রপ একটি প্রদাহীকরণ না নিয়ে সরাসরি লোকসান ফাংশনের সর্বনিম্ন দিকে এগিয়ে যায়।

এখন পর্যন্ত আমরা সেই গতির দিকের দিকে ওজন পরামিতি আপডেট করতে গ্রেডিয়েন্টের বেগ তৈরি করতে মুহূর্ত শব্দটি ব্যবহার করেছি। অ্যাডগ্রাড এবং আরএমএসপ্রপের ক্ষেত্রে আমরা বর্তমান গ্রেডিয়েন্টটি স্কেল করতে স্কোয়ার গ্রেডিয়েন্টের যোগফল ব্যবহার করেছি, তাই আমরা প্রতিটি মাত্রায় একই অনুপাত সহ ওজন আপডেট করতে পারি। এই দুটি পদ্ধতি বেশ ভাল ধারণা বলে মনে হয়েছিল। কেন আমরা কেবল উভয় পৃথিবীর সেরাটি গ্রহণ করি না এবং এই ধারণাগুলি একটি একক অ্যালগরিদমের সাথে একত্রিত করি না?

এটি হ'ল অ্যাডাম নামক চূড়ান্ত অপ্টিমাইজেশনের অ্যালগরিদমের পিছনের সঠিক ধারণা যা আমি আপনাকে পরিচয় করিয়ে দিতে চাই।

অ্যালগরিদমের মূল অংশটি নিম্নলিখিত তিনটি সমীকরণ নিয়ে গঠিত। এই সমীকরণগুলি প্রথমে অপ্রতিরোধ্য মনে হতে পারে তবে আপনি যদি ঘনিষ্ঠভাবে তাকান তবে আপনি পূর্বের অপ্টিমাইজেশন অ্যালগরিদমের সাথে কিছুটা পরিচিতি দেখতে পাবেন।

প্রথম সমীকরণটি কিছুটা গতিযুক্ত এসজির মতো দেখায়। এই ক্ষেত্রে,

m  শর্ত  টি হবে বেগ এবং β1 ঘর্ষণ শর্ত।

অ্যাডামের ক্ষেত্রে, আমরা m কে প্রথম গতি বলি এবং β1 কে বলি  একটি হাইপারপ্যারামিটার।

গতিবেগের সাথে SGD র পার্থক্যটি হ'ল ফ্যাক্টর (1- β1), যা বর্তমান গ্রেডিয়েন্টের সাথে গুণিত হয়।

অন্যদিকে সমীকরণের দ্বিতীয় অংশটি আরএমএসপ্রপ হিসাবে বিবেচিত হতে পারে, যেখানে আমরা স্কোয়ার গ্রেডিয়েন্টের চলমান যোগফল রাখছি। এছাড়াও, এই ক্ষেত্রে, ফ্যাক্টর (1-β2) যা স্কোয়ার গ্রেডিয়েন্টের সাথে গুণিত হয়।

সমীকরণের v শর্ত টিকে দ্বিতীয় গতিবেগ হিসাবে ডাকা হয়, এবং β2 এছাড়াও একটি হাইপারপ্যারামিটার। চূড়ান্ত আপডেট সমীকরণটি মোমেন্টামের সাথে আরএমএসপ্রপ এবং এসজিডি সংমিশ্রণ হিসাবে দেখা যেতে পারে।

এখনও অবধি আদম পূর্ববর্তী দুটি অপটিমাইজেশন অ্যালগরিদমের দুর্দান্ত বৈশিষ্ট্যগুলিকে একীভূত করেছে, তবে এখানে কিছুটা সমস্যা রয়েছে এবং এটি শুরুতে কী ঘটে যায় তা নিয়েই প্রশ্ন।

প্রথম বারের ধাপে, প্রথম এবং দ্বিতীয় গতি শর্তগুলি শূন্যে শুরু হয়। দ্বিতীয় গতির প্রথম আপডেটের পরে, এই শর্ত টি এখনও শূন্যের খুব কাছাকাছি। আমরা যখন সর্বশেষ সমীকরণে ওজনের পরামিতিগুলি আপডেট করি তখন আমরা একটি খুব ছোট দ্বিতীয় গতিবেগের শর্ত  v দ্বারা ভাগ করি, যার ফলে খুব বড় প্রথম ধাপ আপডেটের  হয়।

এই প্রথম খুব বড় আপডেটের পদক্ষেপটি সমস্যার জ্যামিতির ফলাফল নয়,

তবে এটি সত্যের একটি নিদর্শন যে আমরা প্রথম এবং দ্বিতীয় গতি শূন্যে শুরু করেছি। প্রথম প্রথম আপডেটের বড় পদক্ষেপগুলির সমস্যাগুলি সমাধান করার জন্য, অ্যাডাম একটি সংশোধন ধারাটি অন্তর্ভুক্ত করেছে:

আপনি দেখতে পাচ্ছেন যে প্রথম এবং দ্বিতীয় গতির মি এবং ভি এর প্রথম আপডেটের পরে আমরা বর্তমান সময়ের পদক্ষেপ টি বিবেচনায় নিয়ে এই গতিগুলির একটি নিরপেক্ষ অনুমান করি। এই সংশোধন শর্তাদি প্রথম এবং দ্বিতীয় গতির মানগুলি পক্ষপাত সংশোধন ছাড়াই মামলার তুলনায় প্রথম দিকে উচ্চতর করে তোলে।

ফলস্বরূপ, নিউরাল নেটওয়ার্ক প্যারামিটারগুলির প্রথম আপডেটের ধাপটি এত বড় হয় না এবং শুরুতে আমরা আমাদের প্রশিক্ষণটি বিশৃঙ্খলা করি না। অতিরিক্ত পক্ষপাত সংশোধন আমাদের অ্যাডাম অপটিমাইজারের সম্পূর্ণ ফর্ম দেয়।

এখন, আমাদের ক্ষতি ফাংশনের বিশ্বব্যাপী সর্বনিম্ন খুঁজে বের করার পরিপ্রেক্ষিতে একে অপরের সাথে সব আলগোরিদিম তুলনা যাক:

অবশেষে, আমরা সেরা গ্রেডিয়েন্ট বংশদ্ভুত অ্যালগরিদম কী তা নিয়ে প্রশ্নটি আলোচনা করতে পারি।

সাধারণভাবে, একটি সাধারণ গ্রেডিয়েন্ট বংশদ্ভুত অ্যালগরিদম সহজ কাজের জন্য পর্যাপ্ত চেয়ে বেশি। আপনি যদি আপনার মডেলের যথার্থতার সাথে সন্তুষ্ট না হন তবে আপনি আরএমএসপ্রপ চেষ্টা করে দেখতে পারেন বা আপনার গ্রেডিয়েন্ট বংশদ্ভুত অ্যালগরিদমে একটি গতিময় পদ যুক্ত করতে পারেন।

তবে আমার অভিজ্ঞতায় নিউরাল নেটওয়ার্কগুলির জন্য সর্বোত্তম অপ্টিমাইজেশনের অ্যালগরিদম হ'ল আদম। এই অপটিমাইজেশন অ্যালগরিদম আপনার যে কোনও deep  learning  সমস্যার মুখোমুখি হবে না তার জন্য খুব ভাল কাজ করে। Especially if you set the hyperparameters to the following values:

… this would be a very good starting point for any problem and virtually every type of neural network architecture I’ve ever worked with.

এজন্য আমি যে প্রতিটি সমস্যার সমাধান করতে চাইছি তার জন্য অ্যাডাম অপটিমাইজার হ'ল আমার ডিফল্ট অপ্টিমাইজেশন অ্যালগরিদম।

কেবল খুব কম ক্ষেত্রেই আমি অন্যান্য অপ্টিমাইজেশান অ্যালগরিদমগুলিতে স্যুইচ করি যা আমি আগে পরিচয় করিয়েছি।

এই অর্থে, আমি আপনাকে পরামর্শ দিচ্ছি যে আপনি যে সমস্যাটি নিয়ে কাজ করছেন সেই ডোমেনের নিউরাল নেটওয়ার্কের আর্কিটেকচার নির্বিশেষে আপনি সর্বদা অ্যাডাম অপটিমাইজারের সাথে শুরু করুন।