তুমি তোমার আম্মুকে কতটুকু ভালোবাসো?
অনে…ক। তবে মাপা যায়না।
ক্রিকেট খেলা কতটুকু পছন্দ করো?
মোটামুটি। এটাও মাপা যায়না।
রাজনীতি পছন্দ করো?
মোটেও না। বরং অপছন্দ করি। কতটুকু করি সেটাও মাপা যায়না।
তোমার ভর কত?
আজকাল মোটা হয়ে গেছি। ৮৭ কেজি! তারমানে মাপা যায়।
আজকে অনেক গরম। আজকের তাপমাত্রা কত?
হুঁ, অনেক গরম পড়েছে। ৩৫ ডিগ্রি সেলসিয়াস। তারমানে এটাও মাপা যায়।
এভাবে অসংখ্য উদাহরণ দেয়া যায়। এই উদাহরণগুলোর মধ্যে আমরা স্পষ্টত দুটো দল বা ভাগ পাবো। একদলকে পরিমাপ করা যায় না এবং আরেক দলকে পরিমাপ করা যায়। যাদের পরিমাপ করা যায়, তাদেরকে রাশি বলে।
এবার তাহলে রাশি নিয়ে আরও কথা বলা যাক। মনে করি, হাসান নামে একজন স্কুলে পড়ে। তার বাড়ি থেকে স্কুল ২ কিলোমিটার দূরে। নিচের ছবিটা খেয়াল করি।

এখন হাসান যদি বাড়ি থেকে বের হয়ে যেকোন দিকে ২ কিলোমিটার রাস্তা যায়, সে কি স্কুল খুঁজে পাবে? মোটেও না। তাকে অবশ্যই একটা নির্দিষ্ট দিকেই যেতে হবে। এই উদাহরণে, হাসানকে অবশ্যই ২ কিলোমিটার পশ্চিমে যেতে হবে। এখানে রাস্তার দৈর্ঘ্য মাপা গেছে (২ কিলোমিটার), তাই অবশ্যই এটা একটা রাশি। এখন আমরা দেখবো, এই রাশির কয়টা অংশ আছে। আবারও নিচের ছবিটা খেয়াল করি।

তাহলে আমাদের আলোচ্য রাশিটাকে প্রকাশ করতে গেলে তিনটা অংশের প্রয়োজন পড়ছে। যে কোনো একটা অংশ বাদ দিলেই হাসান স্কুল পৌঁছাতে পারবেনা। আমি যদি ‘২’ এর জায়গায় ‘৩’ বলি তাহলেও হবেনা; ‘কিলোমিটার’ এর জায়গায় মিটার বা গজ বলি তাহলেও হবেনা কিংবা ‘পশ্চিম’ এর জায়গায় ‘পূর্ব’ বলি তাহলেও হবেনা।
সুতরাং বলা যায় যে, আমাদের আলোচ্য রাশিটা এমন একটা রাশি যেটা প্রকাশ করতে গেলে মান, একক ও দিকের প্রয়োজন হয়।
আচ্ছা, হাসানের দাদুর ডায়াবেটিস আছে। ডায়াবেটিস এমন একটা রোগ, যেটা শুধু ওষুধ খেলেই সেরে যায় না। বরং ওষুধের পাশাপাশি খাওয়া দাওয়া মেনে বেছে করা লাগে এবং সাথে সাথে হাঁটাহাঁটি করা লাগে। তো হাসানের দাদুকে ডাক্তারবাবু বলেছেন, আপনি প্রতিদিন ২ কিলোমিটার হাঁটবেন।
ডাক্তার নিশ্চয়ই দাদুকে বলবেনা যে, আপনি খবরদার পূর্ব দিকে হাঁটবেন না; পশ্চিম দিকে হাঁটবেন, নাহলে আপনার ডায়াবেটিস বেড়ে যাবে। এরকম কথা নিশ্চয়ই কোন ডাক্তারই বলবেন না। হাসানের দাদুর যেদিকে ইচ্ছা তিনি হাঁটতে পারেন।
তাহলে আমরা দেখতে পাচ্ছি যে, দাদুর হাঁটাহাঁটির ক্ষেত্রে ‘দিক’ টা উল্লেখযোগ্য না। শুধু ‘মান’ ও ‘একক’ উল্লেখযোগ্য। এবার তাহলে আমরা উপরের আলোচনার ওপর ভিত্তি করে একটা টেবিল বানিয়ে ফেলি।
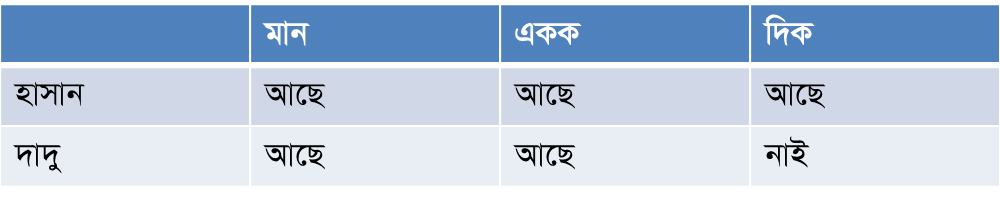
এখান থেকে বলা যায় যে, ‘দিক’ এর উপর ভিত্তি করে রাশিকে দুইভাগে ভাগ করা যায়। একদলের ‘দিক’ আছে এবং আরেকদলের ‘দিক’ নাই। তাহলে ‘দিক’ এর ওপর ভিত্তি করে রাশি দুই প্রকার। যথা:
১। দিকওয়ালা রাশি (ভেক্টর)
২। দিকছাড়া রাশি (স্কেলার)
ভেক্টর রাশি: যেসকল রাশিকে সম্পূর্ণভাবে প্রকাশ করার জন্য মান ও দিক উভয়ের প্রয়োজন হয়, তাদেরকে ভেক্টর রাশি বলে।
অবশেষে ভেক্টরকে ডাকাডাকি করে ভেক্টরের খোঁজ পাওয়া গেল। এবার যাই, ম্যাট্রিক্স কার বাড়ি গেলো খুঁজে নিয়ে আসি। আসো আমার সাথে।
আমাদের বীজগণিত পড়া শুরু হয় বেশ ছোট ক্লাস থেকেই। সেটা কত ছোট এ মুহূর্তে মনে পড়ছে না। ক্লাস সেভেন-এইট থেকে হয়তো। তারমানে আমি ধরে নিচ্ছি তুমি বীজগণিতের সমীকরণের সাথে পরিচিত। উদাহরণ দেখি,
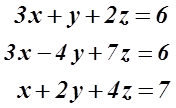
এখন যদি তোমরাকে বলা হয় যে, উপরের তিনটা সমীকরণ সমাধান করে x, y, z এর মান বের করে ফেলো। আমার ধারণা তোমরা ঝটপট করে ফেলতে পারবা।
আচ্ছা এখন আমি একটা কাজ করবো। উপরের সমীকরণ তিনটাকেই আবার লেখবো, তবে একটু অন্য ঢং এ। অর্থাৎ ঐ একই জিনিসই লিখবো তবে প্রকাশভঙ্গিটা একটু আলাদা আরকি!
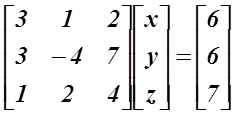
তোমরা বিশ্বাস করো, উপরের তিনটা সমীকরণ আর এইযে বিদঘুটে চারকোণা বক্সগুলোর মধ্যে যা লিখেছি, তা একই জিনিস। শুধু প্রকাশভঙ্গিটা আলাদা। এই প্রকাশ ভঙ্গিটাকেই ম্যাট্রিক্স বলে। এখানে ছোট-বড় তিনটা বক্সের মতো আছে, তারমানে এখানে তিনটা ম্যাট্রিক্স আছে।
এখানে আসলে আমরা কি করেছি?
x এর সাথে যে সংখ্যাগুলো (এদেরকে x এর সহগ বলে) আছে তাদেরকে লম্বা করে দাঁড় করিয়ে দিয়েছি, আবার তারপাশে y এর সহগ এবং শেষে z এর সহগ দিয়ে একটা ম্যাট্রিক্স বানিয়েছি। এই ম্যাট্রিক্সের সাথে x, y, z দিয়ে একটি ম্যাট্রিক্স বানিয়ে গুণ দেয়া হয়েছে। শেষে সমান চিহ্নের ডানপাশে যে সংখ্যাগুলো ছিল সেগুলো এখানেও রাখা হয়েছে, তবে ম্যাট্রিক্সরূপে।
আরেকটা উদাহরণ দেখা যাক, তাহলে ব্যাপারটা আরও পরিষ্কার হবে।
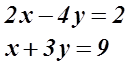
এটাকে যদি আগের মতো করে ম্যাট্রিক্স দিয়ে প্রকাশ করি তাহলে দাঁড়াবে,
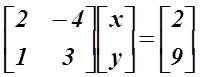
এখন আমরা ম্যাট্রিক্সের কিছু জিনিসপত্র শিখবো।
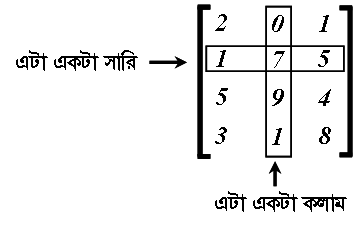
তাহলে উপরের ম্যাট্রিক্সটাতে ৪ টা সারি এবং ৩ টা কলাম আছে। এই ম্যাট্রিক্সকে আমরা ৪*৩ (উচ্চারণঃ ফোর বাই থ্রি ম্যাট্রিক্স, একে আমরা ম্যাট্রিক্সের ক্রম বা order বলে থাকি) বলতে পারি। নিয়মটা হচ্ছে, আগে সারির সংখ্যা এবং পরে কলামের সংখ্যা বলতে হয়। আর এদের মাঝে যে গুণ চিহ্ন দেয়া আছে, সেটা আসলে গুণ নয়। ওটা উচ্চারণ করতে হয় ‘বাই’।
এবার ম্যাট্রিক্সের কিছু প্রকারভেদ দেখে নেয়া যাক।
(১) বর্গ ম্যাট্রিক্সঃ যে ম্যাট্রিক্সের সারি ও কলাম সংখ্যা সমান, তাকে বর্গ ম্যাট্রিক্স বলে। যেমন, ২*২ ম্যাট্রিক্স, ৫*৫ ম্যাট্রিক্স ইত্যাদি।
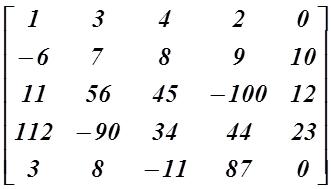
(২) সারি ম্যাট্রিক্সঃ যে ম্যাট্রিক্সে একটিমাত্র সারি থাকে (সাথে যেকোন সংখ্যক কলাম থাকতে পারে, সমস্যা নাই), তাকে সারি ম্যাট্রিক্স বলে। যেমন,
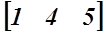
(৩) কলাম ম্যাট্রিক্সঃ অনুরূপভাবে, যে ম্যাট্রিক্সে একটিমাত্র কলাম থাকে, তাকে কলাম ম্যাট্রিক্স বলে। যেমন,
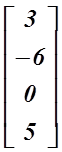
(৪) কর্ণ ম্যাট্রিক্সঃ কোনো ম্যাট্রিক্সকে কর্ণ ম্যাট্রিক্স হতে গেলে অবশ্য একটা শর্ত আছে। সেটা হচ্ছে, প্রথমে তাকে বর্গ ম্যাট্রিক্স হতে হবে। তাহলে কোন বর্গ ম্যাট্রিক্সের যদি শুধু কর্ণ বরাবর উপাদানগুলো অশূন্য হয় এবং বাকি সব উপাদান শূন্য হয়, তবে তাকে কর্ণ ম্যাট্রিক্স বলে। যেমন,
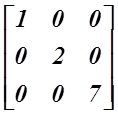
(৫) স্কেলার ম্যাট্রিক্সঃ কোনো ম্যাট্রিক্সকে স্কেলার ম্যাট্রিক্স হতে গেলেও শর্ত আছে। সেটা হচ্ছে যে ম্যাট্রিক্সটিকে প্রথমে কর্ণ ম্যাট্রিক্স হতে হবে। আচ্ছা তাহলে যদি কোন কর্ণ ম্যাট্রিক্সের সব উপাদানগুলো একই হয়, তাহলে সেই ম্যাট্রিক্সকে স্কেলার ম্যাট্রিক্স বলে। যেমন,
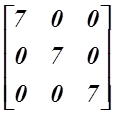
(৬) অভেদক ম্যাট্রিক্সঃ এই ম্যাট্রিক্স হতে গেলে আবার প্রথমে একে স্কেলার ম্যাট্রিক্স হতে হবে। জীবন শর্তময়! তাহলে যে স্কেলার ম্যাট্রিক্সের সবগুলো উপাদান ‘১’ (এক), তাকে অভেদক ম্যাট্রিক্স (Identity Matrix) বলে। যেমন,
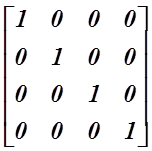
(৭) ট্রান্সপোজ ম্যাট্রিক্সঃ যদি কোন ম্যাট্রিক্সের সারিগুলোকে কলামে এবং কলামগুলোকে সারিতে পরিণত করে নতুন একটি ম্যাট্রিক্স তৈরি করা হয়, তবে নতুন ম্যাট্রিক্সটিকে আমরা পুরনো ম্যাট্রিক্সের ট্রান্সপোজ ম্যাট্রিক্স বলবো। ধরি, A একটি ম্যাট্রিক্স, তাহলে এর ট্রান্সপোজ ম্যাট্রিক্সকে আমরা A^T দিয়ে প্রকাশ করবো। যেমন,

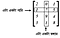
এবার গুরুত্বপূর্ণ একটা কথা। মনে করি, আমার কাছে একটা ম্যাট্রিক্স আছে।
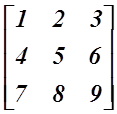
আমরা দেখতে পাচ্ছি, এই ম্যাট্রিক্সের ৩ টা সারি ও ৩ টা কলাম আছে। অর্থাৎ এই ম্যাট্রিক্সের ক্রম হচ্ছে ৩*৩। আমরা যদি এখন এই ম্যাট্রিক্সের প্রতিটা কলামকে আলাদা আলাদা করে লিখি, যেমন,
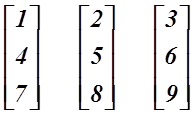
তাহলে এদের প্রত্যেককে আমরা এক একটা কলাম ভেক্টর বলে ডাকবো। এখন প্রশ্ন হচ্ছে, আমরা প্রথমে যে ভেক্টর সম্পর্কে পড়েছি, তার সাথে এই ভেক্টরের কোন সম্পর্ক আছে কিনা? আমরা ধীরে ধীরে সব প্রশ্নের উত্তর পেয়ে যাবো।


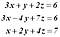
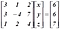
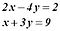
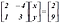
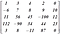
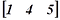
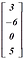
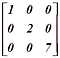
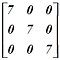
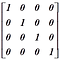

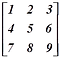
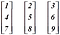
0 comments:
Post a Comment