Gradient descent একটি অপ্টিমাইজেশান অ্যালগরিদম যা বিভিন্ন ML অ্যালগরিদমগুলিতে খরচ ফাংশনটি কমিয়ে আনার জন্য ব্যবহৃত হয়। এখানে কিছু সাধারণ Gradient descent অপ্টিমাইজেশান অ্যালগরিদম রয়েছে যা জনপ্রিয় Deep Learning ফ্রেমওয়ার্কগুলিতে ব্যবহৃত হয়েছে যেমন টেন্সরফ্লো এবং কেরাস।
Gradient descent একটি অপ্টিমাইজেশান পদ্ধতি ফাংশন সর্বনিম্ন খুঁজে বের করার জন্য। এটি সাধারণত ব্যাকপ্রোপাগেশনের মাধ্যমে নিউরাল নেটওয়ার্কের ওজন আপডেট করতে deep learning মডেলগুলিতে ব্যবহৃত হয়।
এই পোস্টে, আমি জনপ্রিয় DEEP lEARNING ফ্রেমওয়ার্কগুলিতে ব্যবহৃত সাধারণ Gradient descent অপ্টিমাইজেশান অ্যালগরিদমগুলি সংক্ষিপ্ত করব (e.g. TensorFlow, Keras, PyTorch, Caffe) (উদাঃ টেন্সরফ্লো, কেরাস, পাইটোচ, ক্যাফ)। এই পোস্টটির উদ্দেশ্যটি সহজে পড়তে এবং ডাইজেস্ট করা (সামঞ্জস্যপূর্ণ নামকরণের মাধ্যমে) সেখানে অনেকগুলি সারসংক্ষেপ নেই এবং চিট শীট হিসাবে যদি আপনি স্ক্র্যাচ থেকে তাদের বাস্তবায়ন করতে চান তবে তা হ'ল।
আমি জাভাস্ক্রিপ্ট ব্যবহার করে এখানে গ্রেডিয়েন্ট বংশের ডেমো ব্যবহার করে একটি রৈখিক প্রতিক্রিয়া সমস্যাতে SGD, momentum, নেস্টেরভNesteov, RMSProp এবং Adam বাস্তবায়িত করেছি।
কি করে Gradient desceni optimisers করবেন?
(1) modifying the learning rate component, α, or
(2) modifying the gradient component, ∂L/∂w, or
(3) both.
(2) modifying the gradient component, ∂L/∂w, or
(3) both.
See the last term in Eqn. 1 below:
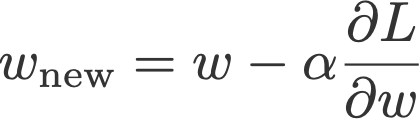
Eqn. 1: The terms in stochastic gradient descent
Learning rate schedulers vs. Gradient descent optimisers
এই দুইটির মধ্যে প্রধান পার্থক্য হল গ্রেডিয়েন্ট বংশের অপটিমাইজারগুলি শিক্ষার হারকে গ্র্যাডিয়েন্টগুলির একটি ফাংশন দিয়ে গুণ দ্বারা গুণমানের গুণগত মান বাড়িয়ে তুলবে এবং লার্নিং রেট অনুস্মারকগুলি একটি ধ্রুবক বা একটি ফাংশন দ্বারা শিক্ষার হারকে গুণিত করবে ধাপে ধাপে।
For (1) এই অপ্টিমাইজারগুলি শেখার হারের জন্য একটি positive ফ্যাক্টর গুণ করে তারা ছোট হয়ে যায়। For (2) অপটিমাইজারগুলি সাধারণত ভ্যানিলা Gradent descent মতো একটি মান গ্রহণের পরিবর্তে গ্রেডিয়েন্ট (Momentum) এর চলমান গড়ের ব্যবহার করে। (3) Adam and AMSGrad যে অপ্টিমাইজার উভয় কাজ ।
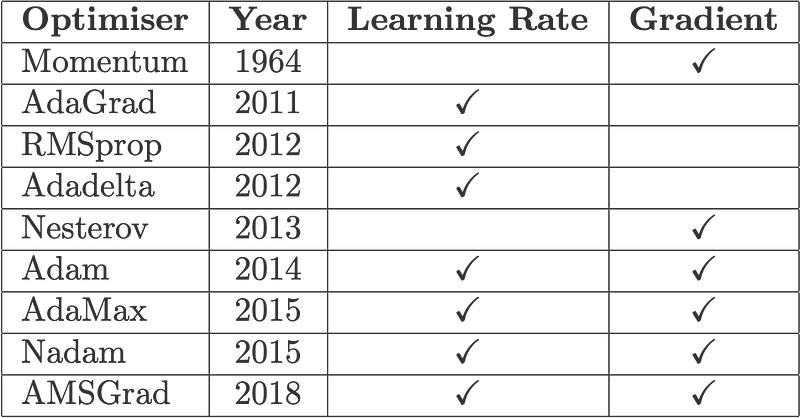
Fig. 2: Gradient descent optimisers, the year in which the papers were published, and the components they act upon.
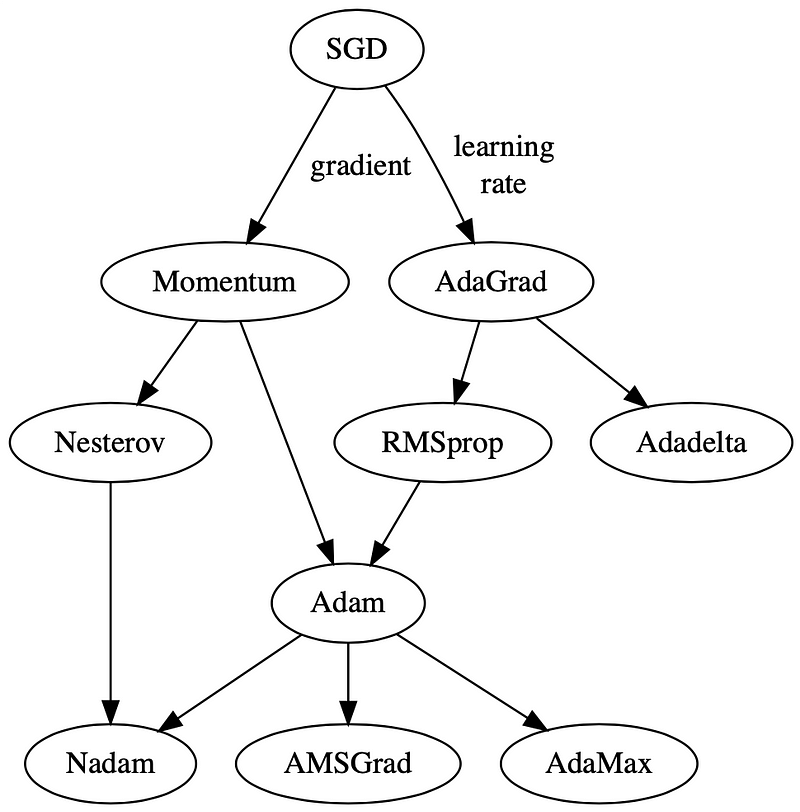
চিত্র 3। এই অপ্টিমাইজারগুলি কীভাবে ADAM রূপ থেকে নিচে, simple vanilla stochastic gradient descent (SGD) থেকে বিকাশ ঘটেছে তার একটি বিবর্তনীয় মানচিত্র। SGD প্রাথমিকভাবে দুটি প্রধান ধরণের অপ্টিমাইজারে বিভক্ত: যারা (i) the learning rate component, through momentum and (ii) the gradient component, through AdaGrad.Down the generation line, we see the birth of Adam (pun intended 😬), a combination of momentum and RMSprop, a successor of AdaGrad. You don’t have to agree with me, but this is how I see them 🤭.
Notations
- t — time step
- w — weight/parameter which we want to update
- α — learning rate
- ∂L/∂w — gradient of L, the loss function to minimise, w.r.t. to w
- I have also standardised the notations and Greek letters used in this post (hence might be different from the papers) so that we can explore how optimisers ‘evolve’ as we scroll.
Content
- Stochastic Gradient Descent
- Momentum
- NAG
- AdaGrad
- RMSprop
- Adadelta
- Adam
- AdaMax
- Nadam
- AMSGrad
1. Stochastic Gradient Descent
The vanilla gradient descent updates the current weight wt using the current gradient ∂L/∂wtmultiplied by some factor called the learning rate, α.
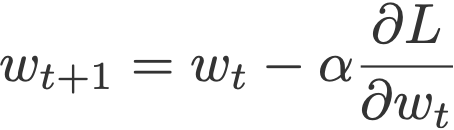
2. Momentum মুহূর্ত
ওজন হালনাগাদ করার জন্য বর্তমান গ্রেডিয়েন্টের উপর নির্ভর করে পরিবর্তনের সাথে গ্রেডিয়েন্ট বংশবৃদ্ধি (Polyak, 1964) বর্তমান গ্রেডিয়েন্টকে Vt (which stands for velocity), দিয়ে প্রতিস্থাপন করে, বর্তমান এবং অতীতের গ্রেডিয়েন্টের সূচকীয় চলমান গড় (অর্থাৎ আপ টু টাইম t )। পরে এই পোস্টে, আপনি দেখতে পাবেন যে এই গতি আপডেটটি গ্রেডিয়েন্ট উপাদানটির জন্য আদর্শ আপডেট হয়ে ওঠে

Where
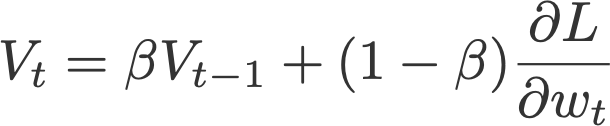
and V initialised to 0.
Common default value:
- β = 0.9
Note that many articles reference the momentum method to the publication by Ning Qian, 1999. However, the paper titled Sutskever et al. attributed the classical momentum to a much earlier publication by Polyak in 1964, as cited above. (Thank you to James for pointing this out.)
3. Nesterov Accelerated Gradient (NAG)
After Polyak had gained his momentum (pun intended 😬), a similar update was implemented using Nesterov Accelerated Gradient (Sutskever et al., 2013). This update utilises V, the exponential moving average of what I would call projected gradients.

where
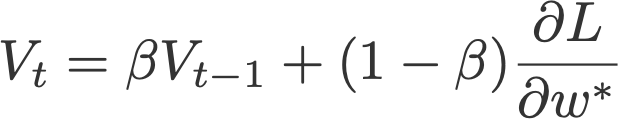
and V initialised to 0.
The last term in the second equation is a projected gradient. This value can be obtained by going ‘one step ahead’ using the previous velocity (Eqn. 4). This means that for this time step t, we have to carry out another forward propagation before we can finally execute the backpropagation. Here’s how it goes:
- Update the current weight wt to a projected weight w* using the previous velocity.
- Carry out forward propagation, but using this projected weight.
- Obtain the projected gradient ∂L/∂w*.
- Compute Vt and wt+1 accordingly.
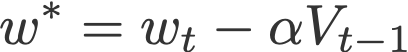
Common default value:
- β = 0.9
Note that the original Nesterov Accelerated Gradient paper (Nesterov, 1983) was not about stochastic gradient descent and did not explicitly use the gradient descent equation. Hence, a more appropriate reference is the above-mentioned publication by Sutskever et al. in 2013, which described NAG’s application in stochastic gradient descent. (Again, I’d like to thank James’s comment on Hacker News for pointing this out.)
4. AdaGrad
Adaptive gradient, or AdaGrad (Duchi et al., 2011), works on the learning rate component by dividing the learning rate by the square root of S, which is the cumulative sum of current and past squared gradients (i.e. up to time t). Note that the gradient component remains unchanged like in SGD.

where
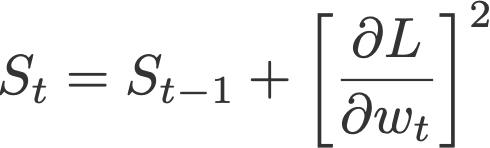
and S initialised to 0.
Notice that ε is added to the denominator. Keras calls this the fuzz factor, a small floating point value to ensure that we will never have to come across division by zero.
Default values (from Keras):
- α = 0.01
- ε = 10⁻⁷
5. RMSprop
Root mean square prop or RMSprop (Hinton et al., 2012) is another adaptive learning rate that is an improvement of AdaGrad. Instead of taking cumulative sum of squared gradients like in AdaGrad, we take the exponential moving average of these gradients.

where
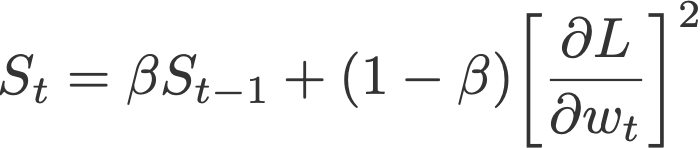
and S initialised to 0.
Default values (from Keras):
- α = 0.001
- β = 0.9 (recommended by the authors of the paper)
- ε = 10⁻⁶
6. Adadelta
Like RMSprop, Adadelta (Zeiler, 2012) is also another improvement from AdaGrad, focusing on the learning rate component. Adadelta is probably short for ‘adaptive delta’, where delta here refers to the difference between the current weight and the newly updated weight.
The difference between Adadelta and RMSprop is that Adadelta removes the use of the learning rate parameter completely by replacing it with D, the exponential moving average of squared deltas.
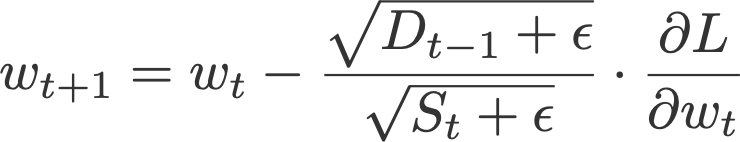
where
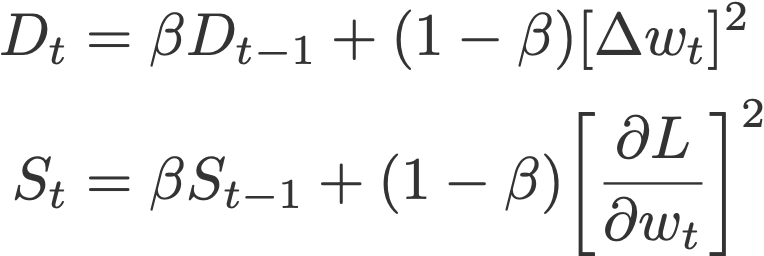
with D and S initialised to 0, and

- β = 0.95
- ε = 10⁻⁶
7. Adam
Adaptive moment estimation, or Adam (Kingma & Ba, 2014), is a combination of momentum and RMSprop. It acts upon
(i) the gradient component by using V, the exponential moving average of gradients (like in momentum), and
(ii) the learning rate component by dividing the learning rate α by square root of S, the exponential moving average of squared gradients (like in RMSprop).
(ii) the learning rate component by dividing the learning rate α by square root of S, the exponential moving average of squared gradients (like in RMSprop).

where
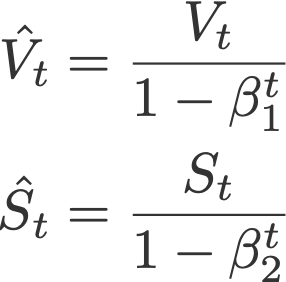
are the bias corrections, and
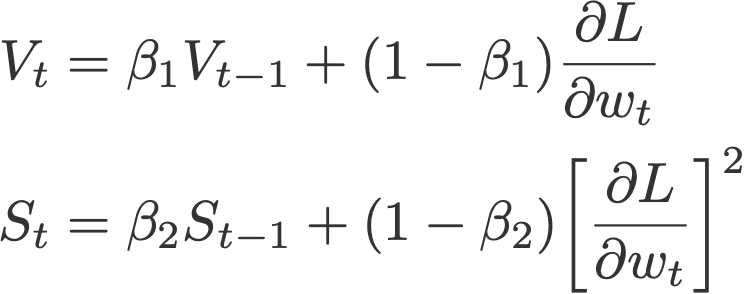
with V and S initialised to 0.
Proposed default values by the authors:
- α = 0.001
- β₁ = 0.9
- β₂ = 0.999
- ε = 10⁻⁸
8. AdaMax
AdaMax (Kingma & Ba, 2015) is an adaptation of the Adam optimiser by the same authors using infinity norms (hence ‘max’). V is the exponential moving average of gradients, and S is the exponential moving average of past p-norm of gradients, approximated to the max function as seen below (see paper for convergence proof).
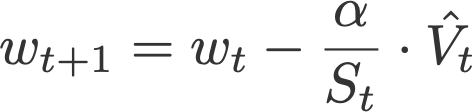
where
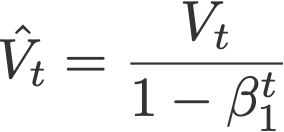
is the bias correction for V and
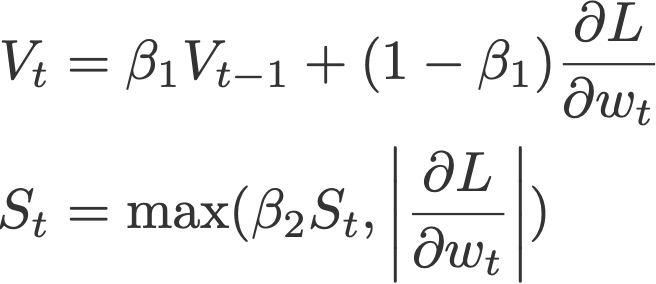
with V and S initialised to 0.
Proposed default values by the authors:
- α = 0.002
- β₁ = 0.9
- β₂ = 0.999
9. Nadam
Nadam (Dozat, 2015) is an acronym for Nesterov and Adam optimiser. The Nesterov component, however, is a more efficient modification than its original implementation.
First we’d like to show that the Adam optimiser can also be written as:
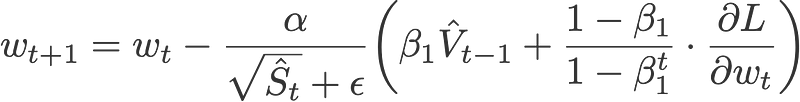
Eqn. 5: Weight update for Adam optimiser
Nadam makes use of Nesterov to update the gradient one step ahead by replacing the previous V_hat in the above equation to the current V_hat:
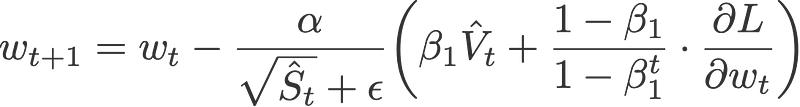
where
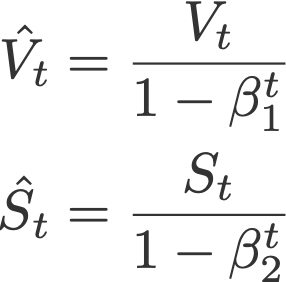
and
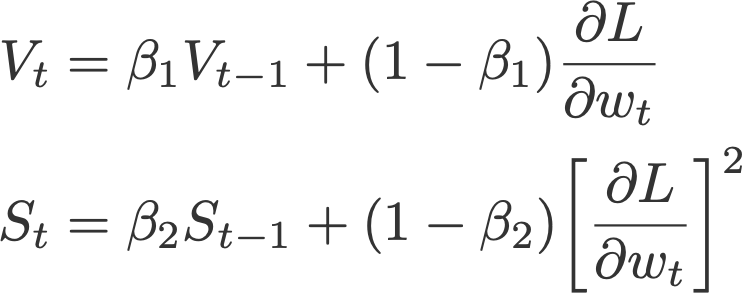
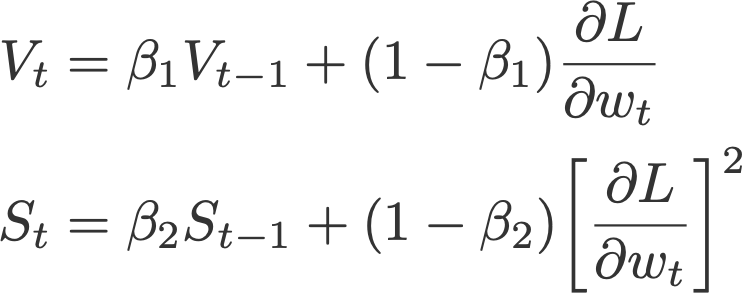
with V and S initialised to 0.
Default values (taken from Keras):
- α = 0.002
- β₁ = 0.9
- β₂ = 0.999
- ε = 10⁻⁷
10. AMSGrad
Another variant of Adam is the AMSGrad (Reddi et al., 2018). This variant revisits the adaptive learning rate component in Adam and changes it to ensure that the current S is always larger than the previous time step.

where
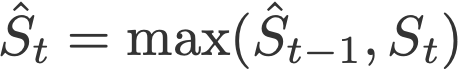
and
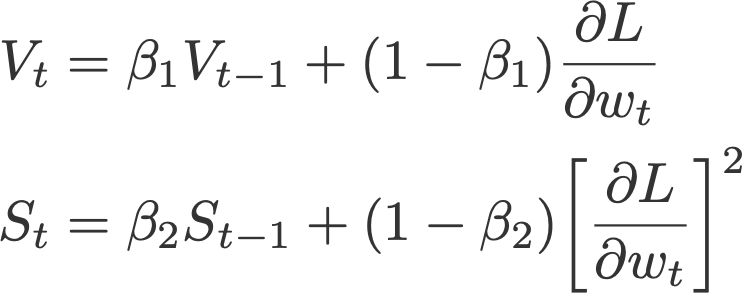
with V and S initialised to 0.
Default values (taken from Keras):
- α = 0.001
- β₁ = 0.9
- β₂ = 0.999
- ε = 10⁻⁷
গ্রেডিয়েন্ট descent অপটিমাইজার গ্রেডিয়েন্ট উপাদানটির জন্য সূচকীয় চলমান গড় এবং শেখার হার উপাদানটির মূল বর্গক্ষেত্র ব্যবহার করে।
ঘন ঘন সূচকীয় চলমান গড় কেন?
আমাদের ওজন হালনাগাদ করতে হবে, এবং তা করার জন্য আমাদের কিছু মান ব্যবহার করতে হবে। আমাদের একমাত্র মান বর্তমান গ্রেডিয়েন্ট, সুতরাং ওজন আপডেট করতে এটি ব্যবহার করা যাক।
কিন্তু শুধুমাত্র বর্তমান গ্রেডিয়েন্ট মান গ্রহণ যথেষ্ট নয়। আমরা আমাদের আপডেট 'ভাল নির্দেশিত' হতে চান। সুতরাং আসুন এছাড়াও আগের gradients অন্তর্ভুক্ত।বর্তমান গ্রেডিয়েন্ট মূল্য এবং অতীতের গ্র্যাডিয়েন্টগুলির তথ্য 'একত্রিত করার' এক উপায় হল যে আমরা সমস্ত অতীত এবং বর্তমান গ্রেডিয়েন্টগুলির একটি সাধারণ গড় নিতে পারি। কিন্তু এই গ্র্যাডিয়েট প্রতিটি সমানভাবে ওজন হয় মানে, এটি স্বজ্ঞাত না কারণ স্পষ্টতই, যদি আমরা সর্বনিম্ন কাছে পৌঁছেছি, তবে সাম্প্রতিকতম গ্রেডিয়েন্ট মানগুলি পূর্বের বেশী তথ্য সরবরাহ করতে পারে।
সুতরাং সবচেয়ে নিরাপদ বাজি হলো আমরা সূচকীয় মুভিং এভারেজ (exponential moving average ) নিতে পারি, যেখানে সাম্প্রতিক গ্রেডিয়েন্ট মানগুলি পূর্বের তুলনায় উচ্চ ওজন (গুরুত্ব) দেওয়া হয়।
কেন রুট দ্বারা শেখার হার বিভক্ত মানে গ্র্যাডিয়েন্ট বর্গক্ষেত্র?
লক্ষ্য শেখার হার উপাদান মাপসই করা হয়। কি আদায় করা? গ্রেডিয়েন্ট। আমাদের নিশ্চিত করতে হবে যে যখন গ্রেডিয়েন্ট বড় হয়, আপডেটটি ছোট (অন্যথায়, একটি বিশাল মান বর্তমান ওজন থেকে বিয়োগ করা হবে!)।
এই প্রভাব তৈরি করার জন্য, অনুকূল শিক্ষার হার পেতে বর্তমান গ্রেডিয়েন্টের দ্বারা α শিক্ষার হারটি ভাগ করে নেবে।
মনে রাখবেন লার্নিং হারের উপাদান সর্বদা ইতিবাচক হওয়া উচিত (কারণ গ্রেডিয়েন্ট উপাদানটির সাথে গুণমানের সময় শেখার হার উপাদানটি পরবর্তীতে একই চিহ্ন থাকা উচিত)। এটা সর্বদা ইতিবাচক নিশ্চিত করতে, আমরা তার পরম মান বা তার বর্গ নিতে পারেন। চলুন বর্তমান গ্রেডিয়েন্টের বর্গক্ষেত্রটি গ্রহণ করি এবং বর্গমূলটি গ্রহণ করে এই বর্গটিকে 'বাতিল' করি।
কিন্তু গতিবেগ মত, বর্তমান গ্রেডিয়েন্ট মান গ্রহণ শুধুমাত্র যথেষ্ট নয়। আমরা আমাদের আপডেট 'ভাল নির্দেশিত' হতে চান। তাই আসুন আগের গ্রিডেন্ট ব্যবহার করা যাক। এবং, উপরে উল্লিখিত হিসাবে, আমরা বর্গমূল ('রুট') গ্রহণ করে, অতএব 'মূল অর্থ বর্গক্ষেত্র' গ্রহণ করে, অতীতের গ্র্যাডেন্টগুলির ('গড় বর্গক্ষেত্র') সূচকীয় চলমান গড় গ্রহণ করব। এই পোস্টে সমস্ত অপ্টিমাইজারগুলি যা লার্নিং হার উপাদানটিতে কাজ করে, এটি অ্যাডগ্র্যাড ব্যতীত (যা স্কয়ারড গ্রেডিয়েন্টগুলির সংযোজনীয় সমষ্টি নেয়)।
Cheat Sheet

Please reach out to me if something is amiss, or if something in this post can be improved! ✌🏼
References
- An overview of gradient descent optimization algorithms (ruder.io)
- Why Momentum Really Works (distill.pub)
0 comments:
Post a Comment