
দুই ধরণের তদারকি করা মেশিন লার্নিং অ্যালগরিদম রয়েছে: রিগ্রেশন এবং শ্রেণিবিন্যাস। পূর্ববর্তীটি অবিচ্ছিন্ন মান আউটপুটগুলির পূর্বাভাস দেয় যখন উত্তরকরা পৃথক পৃথক ফলাফলের পূর্বাভাস দেয়। উদাহরণস্বরূপ, ডলারের বিনিময়ে কোনও বাড়ির দাম সম্পর্কে ভবিষ্যদ্বাণী করা একটি রিগ্রেশন সমস্যা এবং টিউমারটি মারাত্মক বা সৌম্য কিনা তা পূর্বাভাস দেওয়া একটি শ্রেণিবিন্যাস সমস্যা।
এই নিবন্ধে, আমরা সংক্ষেপে অধ্যয়ন করব যে লিনিয়ার রিগ্রেশন কী এবং কীভাবে এটি দু'টি ভেরিয়েবল এবং একাধিক ভেরিয়েবলের জন্য সাইকিট-লার্ন ব্যবহার করে প্রয়োগ করা যেতে পারে, যা পাইথনের অন্যতম জনপ্রিয় মেশিন লার্নিং গ্রন্থাগার।
লিনিয়ার রিগ্রেশন থিওরি
বীজগণিতের "লিনিয়ারিটি" শব্দটি দুই বা ততোধিক ভেরিয়েবলের মধ্যে রৈখিক সম্পর্ককে বোঝায়। আমরা যদি এই সম্পর্কটি একটি দ্বি-মাত্রিক স্থানে (দুটি ভেরিয়েবলের মধ্যে) আঁকি তবে আমরা একটি সরলরেখা পাই।
লিনিয়ার রিগ্রেশন একটি প্রদত্ত স্বতন্ত্র ভেরিয়েবল (এক্স) এর উপর নির্ভরশীল নির্ভরশীল ভেরিয়েবল মান (y) পূর্বাভাস দেওয়ার জন্য কার্য সম্পাদন করে। সুতরাং, এই রিগ্রেশন কৌশলটি এক্স (ইনপুট) এবং y (আউটপুট) এর মধ্যে একটি লিনিয়ার সম্পর্ক সন্ধান করে। সুতরাং, নাম লিনিয়ার রিগ্রেশন। যদি আমরা এক্স অক্ষের উপর স্বতন্ত্র ভেরিয়েবল (x) এবং y- অক্ষের উপর নির্ভরশীল ভেরিয়েবল (y) প্লট করি তবে লিনিয়ার রিগ্রেশন আমাদের জন্য একটি সরল রেখা দেয় যা উপাত্তের পয়েন্টগুলিকে সর্বোত্তমভাবে ফিট করে, যেমন নীচের চিত্রটিতে দেখানো হয়েছে।
আমরা জানি যে একটি সরলরেখার সমীকরণ মূলত হয়

The equation of the above line is :
Y= mx + b
যেখানে বি ইন্টারসেপ্ট এবং এম রেখার opeাল। সুতরাং মূলত, লিনিয়ার রিগ্রেশন অ্যালগরিদম আমাদের ইন্টারসেপ্ট এবং opeাল (দুটি মাত্রায়) জন্য সর্বাধিক অনুকূল মান দেয়। Y এবং x ভেরিয়েবল একই থাকে, যেহেতু সেগুলি ডেটা বৈশিষ্ট্য এবং পরিবর্তন করা যায় না। আমরা যে মানগুলি নিয়ন্ত্রণ করতে পারি সেগুলি হ'ল ইন্টারসেপ্ট (বি) এবং opeাল (এম)। ইন্টারসেপ্ট এবং opeালের মানগুলির উপর নির্ভর করে একাধিক সরল রেখা থাকতে পারে। মূলত লিনিয়ার রিগ্রেশন অ্যালগোরিদম যা করে তা হ'ল এটি ডেটা পয়েন্টগুলিতে একাধিক লাইনের সাথে ফিট করে এবং লাইনটি দেয় যা নিম্নতম ত্রুটির ফলস্বরূপ।
এই একই ধারণাটি এমন ক্ষেত্রে প্রসারিত হতে পারে যেখানে দুটির বেশি ভেরিয়েবল রয়েছে। একে একাধিক লিনিয়ার রিগ্রেশন বলা হয়। উদাহরণস্বরূপ, এমন একটি দৃশ্যের বিষয়ে বিবেচনা করুন যেখানে আপনাকে তার জায়গার উপর ভিত্তি করে বাড়ির দাম, শয়নকক্ষের সংখ্যা, এলাকার মানুষের গড় আয়, বাড়ির বয়স ইত্যাদির উপর পূর্বাভাস দিতে হবে। এই ক্ষেত্রে, নির্ভরশীল ভেরিয়েবল (টার্গেট ভেরিয়েবল) বেশ কয়েকটি স্বতন্ত্র ভেরিয়েবলের উপর নির্ভরশীল। একাধিক ভেরিয়েবল যুক্ত একটি রিগ্রেশন মডেল হিসাবে উপস্থাপিত হতে পারে:
y = b0 + m1b1 + m2b2 + m3b3 + … … mnbn
এটি হাইপারপ্লেনের সমীকরণ। মনে রাখবেন, দুটি মাত্রায় একটি লিনিয়ার রিগ্রেশন মডেল একটি সরল রেখা; তিন মাত্রায় এটি একটি বিমান এবং তিনটি মাত্রার চেয়ে বেশি, একটি হাইপারপ্লেন।
এই বিভাগে, আমরা দেখব যে মেশিন শেখার জন্য পাইথনের সাইকিট-লার্ন গ্রন্থাগারটি রিগ্রেশন ফাংশনগুলি প্রয়োগ করতে কীভাবে ব্যবহার করা যেতে পারে। আমরা দুটি ভেরিয়েবল জড়িত সরল লিনিয়ার রিগ্রেশন দিয়ে শুরু করব এবং তারপরে আমরা একাধিক ভেরিয়েবলগুলি যুক্ত লিনিয়ার রিগ্রেশনটির দিকে এগিয়ে যাব।

দ্বিতীয় বিশ্বযুদ্ধের ডেটাসেটের বিমান বোমা চালানো অভিযানগুলি অন্বেষণ করার সময় এবং স্মরণ করে যে ডি-ডে অবতরণগুলি খারাপ আবহাওয়ার কারণে প্রায় স্থগিত ছিল, বোমা ফাটানো অপারেশন ডেটাসেটের মিশনের সাথে তুলনা করার জন্য আমি এই আবহাওয়ার প্রতিবেদনগুলি পিরিয়ড থেকে ডাউনলোড করেছি
ডেটাসেটটিতে বিশ্বের বিভিন্ন আবহাওয়া স্টেশনে প্রতিদিন রেকর্ড করা আবহাওয়ার পরিস্থিতি সম্পর্কিত তথ্য রয়েছে। তথ্যের মধ্যে বৃষ্টিপাত, তুষারপাত, তাপমাত্রা, বাতাসের গতি এবং দিনটি বজ্রঝড় বা অন্যান্য খারাপ আবহাওয়ার অন্তর্ভুক্ত কিনা তা অন্তর্ভুক্ত।
সুতরাং আমাদের কাজটি সর্বনিম্ন তাপমাত্রা হিসাবে সর্বাধিক তাপমাত্রা গ্রহণ ইনপুট বৈশিষ্ট্যটির পূর্বাভাস দেওয়া।
কোডিং শুরু করা যাক:
সমস্ত প্রয়োজনীয় গ্রন্থাগার আমদানি করুন:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as seabornInstance
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics
%matplotlib inline
The following command imports the CSV dataset using pandas:
dataset = pd.read_csv('/Users/nageshsinghchauhan/Documents/projects/ML/ML_BLOG_LInearRegression/Weather.csv')
Let’s explore the data a little bit by checking the number of rows and columns in our datasets.
dataset.shape
You should receive output as (119040, 31), which means the data contains 119040 rows and 31 columns.
To see the statistical details of the dataset, we can use
describe():dataset.describe()
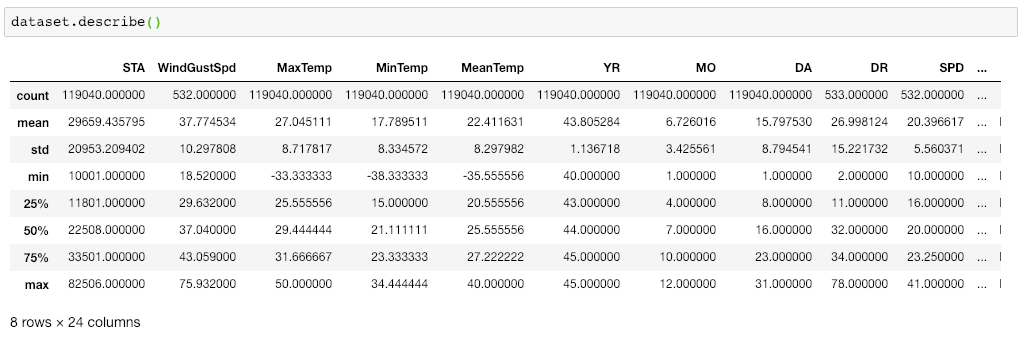
এবং পরিশেষে, আসুন আমাদের ডেটাসেটটি চক্ষু কাটাতে 2-ডি গ্রাফের জন্য আমাদের ডেটা পয়েন্টগুলি প্লট করুন এবং নীচের স্ক্রিপ্টটি ব্যবহার করে আমরা ম্যানুয়ালি ডেটার মধ্যে কোনও সম্পর্ক খুঁজে পেতে পারি কিনা তা দেখুন:
dataset.plot(x='MinTemp', y='MaxTemp', style='o')
plt.title('MinTemp vs MaxTemp')
plt.xlabel('MinTemp')
plt.ylabel('MaxTemp')
plt.show()
We have taken MinTemp and MaxTemp for doing our analysis. Below is a 2-D graph between MinTemp and MaxTemp.

আসুন আমরা সর্বোচ্চ সর্বাধিক তাপমাত্রা যাচাই করি এবং একবার এটি পরিকল্পনা করি আমরা পর্যবেক্ষণ করতে পারি যে গড় সর্বোচ্চ তাপমাত্রা প্রায় 25 এবং 35 এর মধ্যে রয়েছে
plt.figure(figsize=(15,10))
plt.tight_layout()
seabornInstance.distplot(dataset['MaxTemp'])
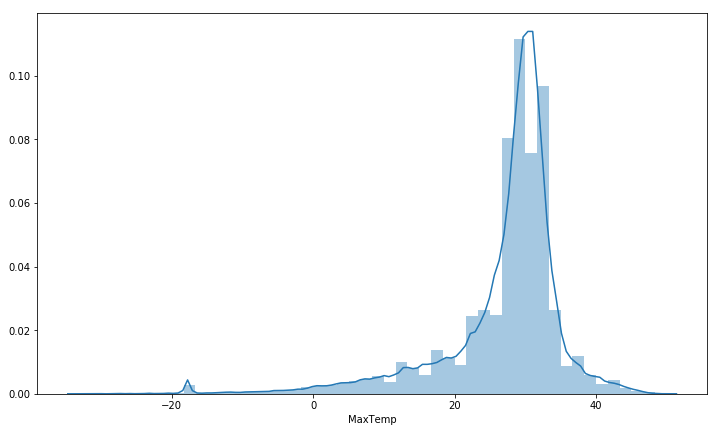
আমাদের পরবর্তী পদক্ষেপটি ডেটাগুলিকে "গুণাবলী" এবং "লেবেলগুলিতে" ভাগ করা।
বৈশিষ্ট্যগুলি হ'ল স্বাধীন ভেরিয়েবলগুলি যখন লেবেলগুলি নির্ভরশীল ভেরিয়েবল যার মানগুলির পূর্বাভাস দেওয়া হয়। আমাদের ডেটাসেটে, আমাদের কেবল দুটি কলাম রয়েছে। আমরা রেকর্ড করা মিনিটেম্পের উপর নির্ভর করে ম্যাক্সটেম্পের পূর্বাভাস দিতে চাই। সুতরাং আমাদের অ্যাট্রিবিউট সেটটিতে "মিনিটেম্প" কলামটি থাকবে যা এক্স ভেরিয়েবলে সঞ্চিত রয়েছে এবং লেবেলটি হবে "ম্যাক্সেম্প" কলাম যা y ভেরিয়েবলে সঞ্চিত।
X = dataset['MinTemp'].values.reshape(-1,1)
y = dataset['MaxTemp'].values.reshape(-1,1)
y = dataset['MaxTemp'].values.reshape(-1,1)
এরপরে, আমরা প্রশিক্ষণের ক্ষেত্রে 80% ডেটা বিভক্ত করি যখন 20% ডেটা নীচের কোড ব্যবহার করে সেট সেট করে।
টেস্ট_সাইজ ভেরিয়েবলটি যেখানে আমরা আসলে পরীক্ষার সেটটির অনুপাত নির্দিষ্ট করি।
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
ডেটা প্রশিক্ষণ এবং পরীক্ষার সেটে বিভক্ত করার পরে, অবশেষে সময়টি হল আমাদের অ্যালগরিদমকে প্রশিক্ষণ দেওয়ার। তার জন্য, আমাদের লিনিয়ারআগ্রেশন ক্লাসটি আমদানি করতে হবে, এটি ইনস্ট্যানিয়েট করতে হবে এবং আমাদের প্রশিক্ষণের ডেটা সহ fit () পদ্ধতিটি কল করতে হবে।
regressor = LinearRegression()
regressor.fit(X_train, y_train) #training the algorithm
regressor.fit(X_train, y_train) #training the algorithm
যেহেতু আমরা আলোচনা করেছি যে লিনিয়ার রিগ্রেশন মডেলটি মূলত intercept and slope র জন্য সর্বোত্তম মান খুঁজে পায়, যার ফলস্বরূপ একটি লাইনের ফলস্বরূপ ডেটা সেরা হয়। দ্বারা খচিত intercept and slope calcul ated-র মান দেখতে আমাদের ডেটাসেটের জন্য লিনিয়ার রিগ্রেশন অ্যালগরিদম, নিম্নলিখিত কোডটি কার্যকর করুন।
#To retrieve the intercept: print(regressor.intercept_)#For retrieving the slope: print(regressor.coef_)

0 comments:
Post a Comment