গ্রিক লজিকে - চিন্তার একটি আদেশ সিস্টেম দেওয়া শর্ত মধ্যে সম্পর্ক তৈরি করে এবং আপনি অনুমানের এবং অনুমান উপর ভিত্তি করে মতামতে উপনীত করতে পারবেন। বেশ প্রায়ই, আমরা একে অপরকে জিজ্ঞাসা: "এটি যৌক্তিক হয়" উত্তর আমাদের অনুমানের নিশ্চিত বা চিন্তার ট্রেন সমালোচনা করেছেন। কিন্তু প্রক্রিয়া সেখানে থামবে না: আমরা কথা বলার জন্য অবিরত।

কখনও কখনও শর্ত (ইনপুট) সংখ্যা এত বড়, এবং তাদের মধ্যে সম্পর্ক তাই বিভ্রান্তিকর এবং জটিল যে মানুষের মস্তিষ্ক একযোগে সমস্ত "হজম" করতে সক্ষম নয়। আপনি কী ঘটছে তা বোঝার জন্য একাধিক মাস (সপ্তাহে, বছর) প্রয়োজন হতে পারে। কিন্তু আধুনিক জীবন আমাদের সিদ্ধান্ত নিতে এই সময় অন্তর দেয় না। এবং আমরা কম্পিউটারের এইড অবলম্বন। এবং এটা এখানে তার আইন এবং বৈশিষ্ট্য সঙ্গে একটি বীজগণিত এবং যুক্তিবিদ্যা আছে, হয়। মূল সমস্ত ডেটা ডাউনলোড করার পর, আমরা কম্পিউটার সব সম্পর্ক চিনতে, অসঙ্গতি দূর করা ও একটি সন্তোষজনক সমাধান খুঁজে বের করার অনুমতি দেয়।

বিখ্যাত Gotfrid Vilgelm Leybnits "গাণিতিক যুক্তিবিজ্ঞান", ধারণা যা কর্ম শুধুমাত্র পণ্ডিতদের একটি ছোট বৃত্ত বুঝতে সহজ ছিল প্রণয়ন। বিশেষ আগ্রহ দিক হতে হয়নি, এবং গাণিতিক যুক্তিবিজ্ঞান কয়েক দ্বারা পরিচিত XIX শতাব্দীর মাঝামাঝি করতে।

বৈজ্ঞানিক সম্প্রদায়ের মহান সুদ একটি বিবাদ যা ইংরেজ Dzhordzh Bul গণিতের একটি শাখা প্রতিষ্ঠা করতে তার অভিপ্রায় ঘোষণা একেবারে কোন ব্যবহারিক প্রয়োগের হচ্ছে না দেখা দেয়। আমরা ইতিহাস থেকে কি জানেন এই সময়ে সক্রিয়ভাবে শিল্প উত্পাদন উন্নয়নশীল, আমরা অক্জিলিয়ারী মেশিন সব ধরণের উন্নত, টি। ই সকল বৈজ্ঞানিক আবিষ্কারের ব্যবহারিক অভিযোজন ছিল।

এগিয়ে খুঁজছি, আমরা বলতে যে একটি বুলিয়ান বীজগণিত - বিশ্বের গণিতের আজ অংশে সর্বাধিক ব্যবহৃত। সুতরাং আপনার যুক্তি Buhl হারিয়ে গেছে।

লেখকের ব্যক্তিত্ব বিশেষ মনোযোগ দাবী করে। এমনকি আসলে অতীত মানুষ আমাদের সামনে বড় হয়েছি, এখনও এটা উল্লেখ করা উচিত যে জন। Buhl 16 বছরের মধ্যে গ্রামের স্কুলে শেখানো, এবং 20 বছর লিঙ্কন তার নিজের স্কুল খোলা দেওয়া। গণিতজ্ঞ পুরোপুরি পাঁচটি বিদেশী ভাষা আয়ত্ত, এবং তার অতিরিক্ত সময়, নিউটন এবং Lagrange কাজ পড়ছিলেন। এবং এই সব - একটি সাধারণ শ্রমিক ছেলে!

1839 সালে Buhl কেমব্রিজ গাণিতিক জার্নালে তার প্রথম বৈজ্ঞানিক কাগজপত্র পাঠানো হয়েছে। সায়েন্টিস্ট 24 বছর পরিণত। Boole এর কাজ রয়েল সোসাইটির তাই আগ্রহী সদস্য, 1844 সালে তিনি উন্নয়নে অবদানের জন্য পদক গ্রহণ করেছেন গাণিতিক বিশ্লেষণ। কয়েক প্রকাশিত কাগজপত্র যা গাণিতিক যুক্তিবিজ্ঞান উপাদান, গণিত কর্ক কাউন্টির কলেজে অধ্যাপক পদে নিতে পারে তরুণ বর্ণনা করা হয়েছে। মনে করে দেখুন যে খুব Boole শিক্ষা ছিলেন না।

বস্তুত, বুলিয়ান বীজগণিত খুব সহজ। আছে বিবৃতি (লজিক্যাল এক্সপ্রেশন) যে, গণিত দৃষ্টিকোণ থেকে মাত্র দুটি শব্দের মধ্যে সংজ্ঞায়িত করা যায়: "সত্য" বা "মিথ্যা"। উদাহরণস্বরূপ, বসন্ত পুষ্প গাছ - সত্য, গ্রীষ্ম এটা বরফ - একটি মিথ্যা। গণিতের সৌন্দর্য এটি কঠোরভাবে প্রয়োজনীয় শুধুমাত্র সংখ্যা ব্যবহার করতে হয় না। বীজগণিত আদালতের রায় জন্য বেশ অনন্য অর্থ সঙ্গে কোনো বিবৃতি মাপসই করা হবে।

সুতরাং, যুক্তির বীজগণিত আক্ষরিক সর্বত্র ব্যবহার করা যেতে পারে: সিডিউলিং এবং লেখা নির্দেশনা, ঘটনা এবং কর্ম ক্রম নির্ধারণ সম্পর্কে পরস্পরবিরোধী তথ্য বিশ্লেষণ। সবচেয়ে গুরুত্বপূর্ণ বিষয় - উপলব্ধি করা এটা কোন ব্যাপার না যে কিভাবে আমরা সত্য বা বিবৃতি মিথ্যা নির্ধারণ করে। থেকে এই "কিভাবে" এবং "কেন" আপনি উপেক্ষা করতে হবে। কি বিষয়ে শুধুমাত্র আসলে এক বিবৃতিতে হল: সত্য একটি মিথ্যা।

অবশ্য, যুক্তিবিদ্যার বীজগণিত যে উপযুক্ত লক্ষণ ও চিহ্ন সঙ্গে রেকর্ড করা হয় সবচেয়ে গুরুত্বপূর্ণ ফাংশন প্রোগ্রামিং। আর তাদের জানুন - এটি একটি নতুন বিদেশী ভাষা শিখতে মানে। কিছুই অসম্ভব।

গভীরতা মধ্যে যাওয়া ছাড়া, আমরা পরিভাষা মোকাবেলা। সুতরাং, বুলিয়ান বীজগণিত presupposes:

বিবৃতি - কোনো সম্মতিসূচক অভিব্যক্তি ব্যাখ্যা করা যেতে পারে যে দুই মূল্যবান। তারা সংখ্যায় (5> 3) অথবা প্রণয়ন পরিচিত শব্দ (- বৃহত্তম স্তন্যপায়ী হাতি) হিসেবে লেখা হয়। এই ক্ষেত্রে, ফ্রেজ এছাড়াও অস্তিত্ব একটি অধিকার রয়েছে, শুধুমাত্র বুলিয়ান বীজগণিত এটা সংজ্ঞায়িত "জিরাফ গলায় নয়" "মিথ্যা।"

সকল বিবৃতি দ্ব্যর্থহীন হওয়া উচিত, কিন্তু তারা মৌলিক বা যৌগিক করা যেতে পারে। সাম্প্রতিক ব্যবহারের যৌক্তিক বান্ডিল। ই বীজগণিত বিবৃতি আদালতের রায় যৌগ প্রাথমিক যুক্তিবিজ্ঞান অপারেশনের উপরন্তু দ্বারা গঠিত হবে।

আমরা ইতিমধ্যে স্মরণ আদালতের রায় বীজগণিত যে অপারেশন - যৌক্তিক। শুধু যোগ, বিয়োগ, বা সংখ্যা তুলনা করতে গাণিতিক অপারেশন ব্যবহার সংখ্যার বীজগণিত যেমন, গাণিতিক যুক্তিবিজ্ঞান উপাদানের জটিল বিবৃতি করতে, অস্বীকার করার বা চূড়ান্ত ফলাফল নিরূপণ করার অনুমতি দেয়।

formalization এবং সরলতা সূত্র, গাণিতিক আমাদের পরিচিত দ্বারা প্রকাশ জন্য লজিক অপারেশন। বুলিয়ান বীজগণিত সমীকরণ প্রোপার্টি এটা সম্ভব রেকর্ড এবং অজানা গণনা করতে ভুলবেন না। লজিক্যাল অপারেশন সাধারণত সত্য সারণী রেকর্ড করা হয়। তার উপাদানের কলাম এবং কম্পিউটিং অপারেশন যা তাদের উপর সঞ্চালিত হয় নির্ধারণ করুন, এবং সারি গণনার ফলাফল দেখাও।

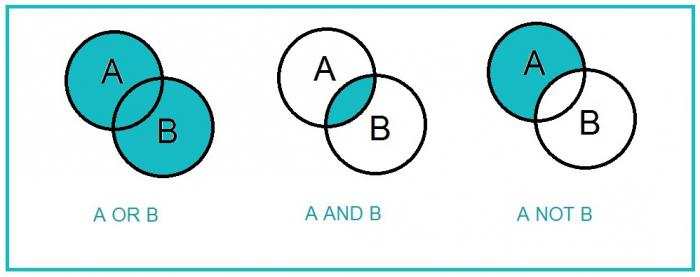
বুলিয়ান বীজগণিত অপারেশনে সবচেয়ে সাধারণ অস্বীকৃতি (না), এবং লজিক্যাল এবং এবং বা। সুতরাং এটি কার্যত বীজগণিত আদালতের রায় সমস্ত ধাপের বর্ণনা করা সম্ভব। আমরা বিস্তারিত গবেষণা তিন অপারেশন প্রতিটি।

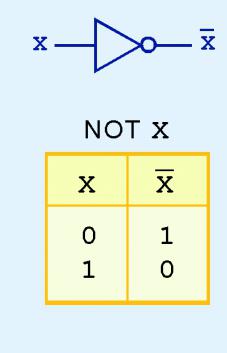
অস্বীকৃতি (নয়) শুধুমাত্র এক উপাদান (প্রতীক) প্রয়োগ করা হয়। অতএব, অপারেশন ইউনারী অস্বীকৃতি বলা হয়। "একটি" ব্যবহার যেমন চিহ্ন ধারণা রেকর্ড করার জন্য: ¬A, A অথবা A !. ট্যাবুলার আকারে এটা ভালো দেখায়:

অস্বীকার থেকে এমন বক্তব্য দি টিপিক্যাল ফাংশন: যদি একটি সত্য হয় তাহলে একটি - মিথ্যা। উদাহরণস্বরূপ, চাঁদ পৃথিবী কাছাকাছি revolves - সত্য; মিথ্যা - পৃথিবীর চাঁদ কাছাকাছি revolves।

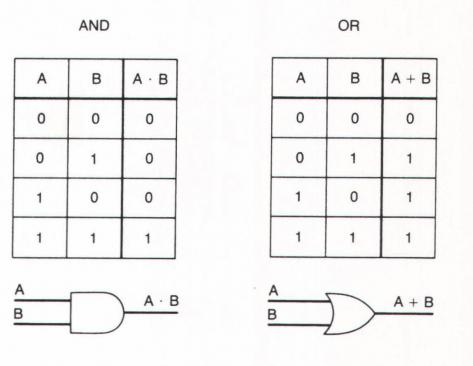
লজিক্যাল এবং অপারেশন একটি সংযোগ বলা হয়। এটা এর অর্থ কি? প্রথমত, এটা দুই operands প্রয়োগ করা যেতে পারে যে, অর্থাত, আমি - .. বাইনারি অপারেশন। দ্বিতীয়ত, এটি শুধুমাত্র উভয় operands (উভয় A এবং B) এর সত্য ক্ষেত্রে সত্য এবং অভিব্যক্তি নিজেই। প্রবাদ, "ধৈর্য এবং একটি সামান্য প্রচেষ্টা" যে বোঝা মাত্র দুটি কারণের একজন ব্যক্তির সমস্যার সঙ্গে মানিয়ে নিতে সাহায্য করতে পারেন।

A∧B, A⋅B বা A && বি: প্রতীক রেকর্ডিং জন্য ব্যবহার করা হয়

সংযোজক অব্যয় গাণিতিক মধ্যে গুণ একই। কখনও কখনও এবং বলে - যৌক্তিক গুণ। আপনি টেবিলের সারি উপাদানের বৃদ্ধি, তাহলে আমরা এর ফলে লজিক্যাল চিন্তা অনুরূপ পেতে।

অসম্বন্ধ একটি লজিক্যাল বা অপারেশন। এটা কি সত্য যদি বিবৃতি অন্তত এক সত্য (হয় A অথবা B) হয়। A∨B, প্রথম সারির B অথবা একটি || বি: এটা মত এই লেখা আছে এসব অস্ত্রোপচারের জন্য সত্য টেবিল আছেন:

অনুরূপ গাণিতিক উপরন্তু অসম্বন্ধ। 1 + 1 টি = 1: যৌক্তিক উপরন্তু অপারেশন শুধুমাত্র একটি সীমাবদ্ধতা আছে। কিন্তু আমরা মনে রাখবেন যে একটি ডিজিটাল ফরম্যাটে গাণিতিক যুক্তিবিজ্ঞান 0 এবং 1 সীমাবদ্ধ (যেখানে 1 - সত্য, 0 - মিথ্যা)। উদাহরণস্বরূপ, বিবৃতি "যাদুঘর আপনি একটি মাষ্টারপিস দেখতে বা একটি ভাল কোম্পানীর জানতে পারেন" অর্থ আপনি শিল্পকর্ম তা দেখতে পারেন, এবং এটি একটি আকর্ষণীয় ব্যক্তি পূরণ করা সম্ভব। একই সময়ে, উভয় ঘটনা যুগপত সিদ্ধি সম্ভাবনা বাতিল হবে না।

সুতরাং, আমরা ইতিমধ্যে কি যৌক্তিক অপারেশন বুলিয়ান বীজগণিত ব্যবহার জানি। কার্যাবলী গাণিতিক যুক্তিবিজ্ঞান উপাদানের সব সম্পত্তি বর্ণনা, এবং আমাদের জটিল যৌগ বিবৃতি প্রক্রিয়া সহজ করার অনুমতি দেয়। সবচেয়ে স্পষ্ট এবং সহজ ডেরাইভেটিভস অপারেশনের প্রত্যাখ্যান সম্পত্তি বলে মনে হয়। দ্বারা ডেরাইভেটিভস XOR যাও, সংশ্লেষ এবং সমানতা বোঝা। যেহেতু আমরা কেবলমাত্র মৌলিক অপারেশন সঙ্গে পড়া আছে, এবং তারপর সম্পত্তি হয় শুধুমাত্র তাদের বিবেচনা।

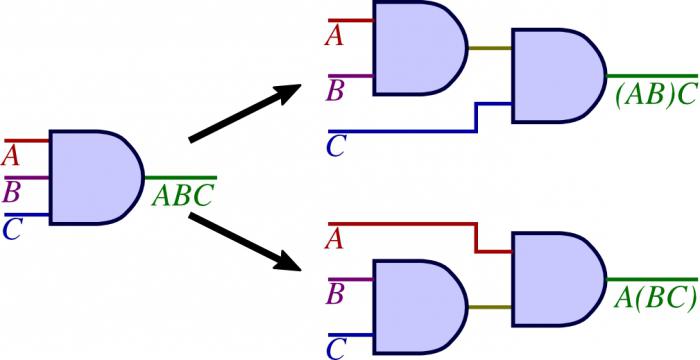
Associativity এর মানে হল যে যেমন বিবৃতির "উভয় A এবং B, এবং বি 'operands ক্রম তালিকা কোন ব্যাপার না। সূত্র নিম্নরূপ লিখিত হয়:

(A∧B) ∧V = A∧ (B∧V) = A∧B∧V,

(A∨B) ∨V = A∨ (B∨V) = A∨B∨V।

যেহেতু আপনি দেখতে পারেন, এই একত্রে কিন্তু একটি বিচ্ছিন্ন অবস্হা অনন্য নয়।

Commutativity যুক্তি দেন যে একত্রে বা অসম্বন্ধ ফল নির্ভর করে না যার উপর আইটেমটি গোড়াতেই হিসেবে বিবেচনা করা হয়:

A∧B = B∧A; A∨B = B∨A।

Distributivity জটিল লজিক্যাল এক্সপ্রেশন মধ্যে বন্ধনী প্রকাশ করতে পারবেন। বিধি গুণ এবং বীজগণিত ছাড়াও উদ্বোধনী প্রথম বন্ধনী অনুরূপ আছেন:

A∧ (B∨V) = A∧B∨A∧V; A∨B∧V = (A∨B) ∧ (A∨V)।

ইউনিট বৈশিষ্ট্য এবং স্ক্র্যাচ, যা হতে পারে operands এক এছাড়াও শূন্য বা এক, এবং একটি একক যোগে দ্বারা বীজগাণিতিক গুণ অনুরূপ আছেন:

A∧0 = 0, A∧1 = a; A∨0 = এ, A∨1 = 1।

Idempotency আমাদের বলে যে যদি অপেক্ষাকৃত দুই সমান operands অপারেশন ফলাফল একই থাকে, তবে আপনি "নিক্ষেপ" বাড়তি জটিলতা দেখা যুক্তি operands পারবেন না। আর একত্রে এবং অসম্বন্ধ অপারেশন idempotent হয়।

B∧B = বি; B∨B = বি

অধিগ্রহণ আমাদের সমীকরণ প্রক্রিয়া সহজ করতে পারবেন। শোষণ যে যখন অভিব্যক্তি এক প্রতীক প্রয়োগ করা হয়, ফলে প্রতীক একই উপাদান সঙ্গে অন্য অপারেশন অপারেশন শুষে করা হয়।

A∧B∨B = বি; (A∨B) ∧B = বি

অপারেশনের ক্রম মহান গুরুত্ব রয়েছে। আসলে, বীজগণিত জন্য, একটি অগ্রাধিকার ফাংশন একটি বুলিয়ান বীজগণিত ব্যবহার করে হয়। সূত্র শুধুমাত্র অপারেশনের তাত্পর্য সাপেক্ষে সরলীকৃত করা যেতে পারে। তুচ্ছ সবচেয়ে উল্লেখযোগ্য এর রাঙ্কিং আমরা ক্রম প্রাপ্ত:

1. অস্বীকার।

2. সংযোজক অব্যয়।

3. অসম্বন্ধ, XOR যাও।

4. সংশ্লেষ, সমানতা।

আপনি দেখতে পারেন, শুধুমাত্র একত্রে অস্বীকৃতি ও সমান অগ্রাধিকার হবে না হিসাবে। অসম্বন্ধ এবং XOR যাও একটি অগ্রাধিকার সমান, সেইসাথে সংশ্লেষ এবং সমানতা অগ্রাধিকার আছে।

আমরা বলেছিলাম যে, মৌলিক যৌক্তিক অপারেশন, গাণিতিক যুক্তিবিজ্ঞান ও ডেরিভেটিভস ব্যবহার আলগোরিদিম তত্ত্ব ছাড়াও। বেশিরভাগ ক্ষেত্রে সংশ্লেষ এবং সমানতা হয়।

সংশ্লেষ বা যৌক্তিক পরিণতি - এই বিবৃতি, যা একটি ক্রিয়া একটি শর্ত, এবং অন্যান্য - তার প্রয়োগের ফলাফল। অন্য কথায়, "যদি ... তারপর" অজুহাতে সঙ্গে এই প্রস্তাব। "রাতের খাবার শেষে হিসাব আসে।" ড্রাইভিং জন্য ই স্লেজগাড়ী পাহাড়ের উপর tightened হবে। যদি কোন পর্বত থেকে নেমে সরানো, এবং তারপর স্লেজগাড়ী টেনে আনতে ইচ্ছা প্রয়োজন নেই। তাই লিখিত: একটি → B অথবা A⇒B।

সমানতা বোঝা নেট প্রভাব যেটা শুধুমাত্র যখন উভয় operands সত্য। উদাহরণ হিসেবে বলা যায়, রাত যখন সূর্য দিগন্ত উপর রি, তারপর দিন উপায় (এবং শুধুমাত্র তারপর) দেয়। এই বিবৃতির গাণিতিক যুক্তির ভাষায় A≡B, A⇔B, একটি == বি যেমন লেখা আছে

বীজগণিত রায় বিকাশ, এবং অনেক আগ্রহী বিজ্ঞানীদের নতুন আইন প্রণয়ন করতে। সবচেয়ে বিখ্যাত বলে মনে করা হয় স্কটিশ গণিতবিদ মন্ত্রণালয় ডি মরগান postulates। তিনি খেয়াল এবং বন্ধ অস্বীকৃতি, উপরন্তু এবং ডাবল নেতিবাচক যেমন বৈশিষ্ট্য একটি সংজ্ঞা দিয়েছেন।

বন্ধ অস্বীকার দাড়ায় যে সামনে প্রথম বন্ধনী কোন আত্মত্যাগী: না (A অথবা B) = না A অথবা বি নয়

যখন প্রতীক অস্বীকার করা হয়, তার মান নির্বিশেষে, উপরন্তু সম্পর্কে বলে,

B∧¬B = 0; B∨¬B = 1।

এবং পরিশেষে, ডবল অস্বীকৃতি নিজেই compensates। অর্থাত সামনে পারেন প্রতীক অস্বীকৃতি disappears অথবা শুধুমাত্র একটি রয়ে যায়।

লজিক বোঝা সরলীকরণ পূর্ব নির্ধারিত সমীকরণ নেই। শুধু মিথ্যা বীজগণিত, এটা সর্বাধিক প্রথম শর্ত সহজতর (জটিল ইনপুট অপারেশন পরিত্রাণ পেতে, এবং তাদের সঙ্গে) প্রয়োজনীয় হয়, তাহলে সঠিক উত্তরের জন্য খুঁজছেন শুরু।

কি প্রক্রিয়া সহজ করার জন্য কি করতে হবে? একটি সহজ অপারেশন সমস্ত ডেরাইভেটিভস রূপান্তর করুন। তাহলে সব বন্ধনী উন্মোচিত (বা তদ্বিপরীত, এই উপাদান কমাতে বন্ধনী করতে)। পরবর্তী ধাপে বাস্তবে বুলিয়ান বীজগণিত বৈশিষ্ট্য ব্যবহার করার জন্য হওয়া উচিত (শোষণ বৈশিষ্ট্য শূন্য এবং এক ও টি।)।

পরিশেষে, সমীকরণ অজানা কমপক্ষে নম্বর, সহজ অপারেশন সঙ্গে মিলিত উপস্থিত থাকা জরুরী। একটি সমাধান জন্য চেহারা করার সবচেয়ে সহজ উপায়, যদি আপনি ঘনিষ্ঠ নেগেটিভ সংখ্যক ভুলবেন না। তারপর উত্তর হিসাবে নিজে যদি পপ আপ করবে।